
 小雨的爸爸从市场买回来四个大西瓜,爸爸为了考一考小雨,让小雨把四个大西瓜依次边上①,②,③,④号后,按质量由小到大的顺序排列出来(不准用称),小雨用一个简易天平操作,操作如下:(操作过程中,天平自身损坏忽略不计)
小雨的爸爸从市场买回来四个大西瓜,爸爸为了考一考小雨,让小雨把四个大西瓜依次边上①,②,③,④号后,按质量由小到大的顺序排列出来(不准用称),小雨用一个简易天平操作,操作如下:(操作过程中,天平自身损坏忽略不计) 解:由题意可得:①>②,②+③>①+④,①+②=③+④,
解:由题意可得:①>②,②+③>①+④,①+②=③+④,

科目:初中数学 来源: 题型:
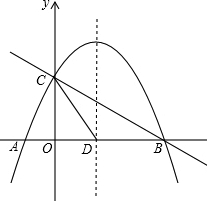 如图,抛物线y=-
如图,抛物线y=-| 4 |
| 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
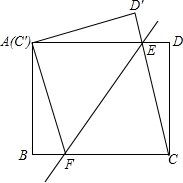 如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E,BC于点F,连接AF、CE.
如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E,BC于点F,连接AF、CE.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com