
分析 (1)类比的出R类整式和QR类整式的定义即可;
(2)类比方法拆开表示得出答案即可;
(3)利用给出的PQR类整式得意义待定得出a、b、c的数值即可.
解答 解:(1)若a=b=0,c≠0,则称该整式为“R类整式”.
若a=0,b≠0,c≠0,则称该整式为“QR类整式”.
(2)∵x2+x+1=(x2+x-1)+(x2-x+1)+(-x2+x+1),
∴该整式为PQR类整式.
(3)∵4x2+11x+2015是“PQR类整式”,
∴设4x2+11x+2015=a(x2+x-1)+b(x2-x+1)+c(-x2+x+1),
∴a+b-c=4,a-b+c=11,-a+b+c=2015,
解得:a=7.5,b=1009.5,c=1013.
点评 此题考查整式,理解题意,掌握给出的整式的特征,利用类比的方法得出答案即可.


科目:初中数学 来源: 题型:填空题
 如图,已知线段AB=6,在平面上有一动点P恒满足PA-PB=4,过点A作∠APB的角平分线的垂线,垂足为M,则△AMB的面积的最大值是6.
如图,已知线段AB=6,在平面上有一动点P恒满足PA-PB=4,过点A作∠APB的角平分线的垂线,垂足为M,则△AMB的面积的最大值是6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
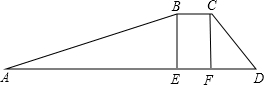 如图所示,拦水坝的横断面为梯形ABCD,斜坡AB的坡度为$\frac{1}{2.5}$,坝顶宽BC=2.8,坝高BE=4.2米,斜坡CD=7.5米.
如图所示,拦水坝的横断面为梯形ABCD,斜坡AB的坡度为$\frac{1}{2.5}$,坝顶宽BC=2.8,坝高BE=4.2米,斜坡CD=7.5米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
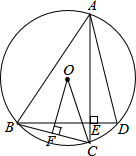 如图.点A、B、C、D在⊙O上,AC⊥BD于点E,过点O作OF⊥BC于F,
如图.点A、B、C、D在⊙O上,AC⊥BD于点E,过点O作OF⊥BC于F,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com