
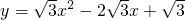 的顶点,B为该抛物线与y轴的交点,C为x轴上一点.设线段BC、AC、AB的长度分别为a、b、c,当a+c=2b时,求:
的顶点,B为该抛物线与y轴的交点,C为x轴上一点.设线段BC、AC、AB的长度分别为a、b、c,当a+c=2b时,求: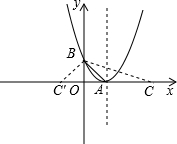 解:(1)∵
解:(1)∵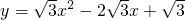 =
= (x-1)2,
(x-1)2, ,即B点坐标为:(0,
,即B点坐标为:(0, ),
),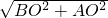 =2,BC=
=2,BC= ,
, ,
, ,x2=1(此时A,C重合不合题意舍去),
,x2=1(此时A,C重合不合题意舍去),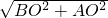 =2,BC′=
=2,BC′=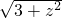 ,
,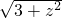 ,
, ,0),
,0), ),
),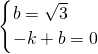 ,
, ,
, x+
x+ ,
, ),
), ,0),
,0),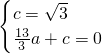
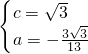 ,
, x+
x+ ;
; ),C点坐标为:(-1,0)时,
),C点坐标为:(-1,0)时, BO×AC′=
BO×AC′= ×2×
×2× =
= ,
, ),C点坐标为:(
),C点坐标为:( ,0)时,
,0)时, -1=
-1= ,
, BO×AC=
BO×AC= ×
× ×
× =
= .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
|
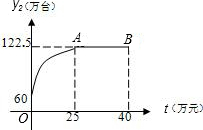 其中点A为抛物线的顶点.
其中点A为抛物线的顶点.查看答案和解析>>
科目:初中数学 来源: 题型:
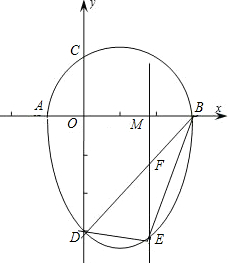 正确?提出你的见解,若△BDE的面积存在最大值,请求出m的值以及点E的坐标.
正确?提出你的见解,若△BDE的面积存在最大值,请求出m的值以及点E的坐标.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com