

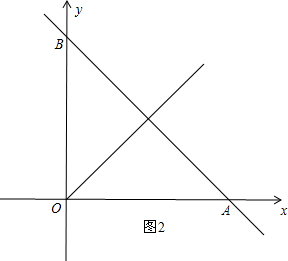
 解:(1)当x=0时,y=4,即B(0,4),
解:(1)当x=0时,y=4,即B(0,4), ,
, ),点D(t,
),点D(t, ).
). =-
=- +4,解得t=4;
+4,解得t=4; =-t+4,解得t=
=-t+4,解得t= .
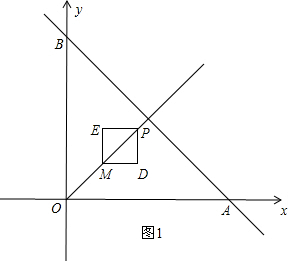
. S=S正方形PDME=DM•PD=(
S=S正方形PDME=DM•PD=( )2=
)2= t2,
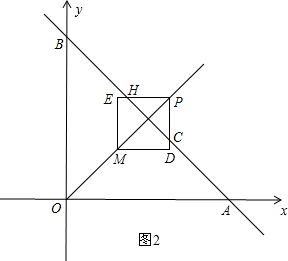
t2, 时,如图2,设直线AB与PD、PE分别交于点C、H.
时,如图2,设直线AB与PD、PE分别交于点C、H. PC2=2(t-2)2;
PC2=2(t-2)2; t2-2(t-2)2=-
t2-2(t-2)2=- t2+8t-8=-
t2+8t-8=- (t-
(t- )2+
)2+ ,
, <
< ,
, 时,Smax=
时,Smax= ;
; ③当
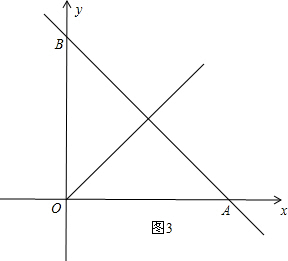
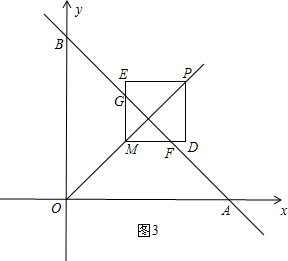
③当 ≤t<4时,如图3,设直线AB与MD、ME分别交于点F、G.
≤t<4时,如图3,设直线AB与MD、ME分别交于点F、G. +4)-
+4)- =-t+4,又MG=MF,
=-t+4,又MG=MF, MG2=
MG2= (t-4)2,
(t-4)2, (t-4)2,
(t-4)2, 时,Smax=
时,Smax= ;
; 时,Smax=
时,Smax= .
. ,
, ),点D(t,
),点D(t, ).先求出当点P在直线AB上时,t=2;当点M在直线AB上时,t=4;当点D在直线AB上时,t=
).先求出当点P在直线AB上时,t=2;当点M在直线AB上时,t=4;当点D在直线AB上时,t= .然后分四种情况进行讨论:①0<t≤2;②2<t<
.然后分四种情况进行讨论:①0<t≤2;②2<t< ;③
;③ ≤t<4;④t≥4.针对每一种情况,分别求出正方形PDME与△OAB公共部分的面积S与t之间的函数关系式,进而求出S的最大值.
≤t<4;④t≥4.针对每一种情况,分别求出正方形PDME与△OAB公共部分的面积S与t之间的函数关系式,进而求出S的最大值.

科目:初中数学 来源: 题型:
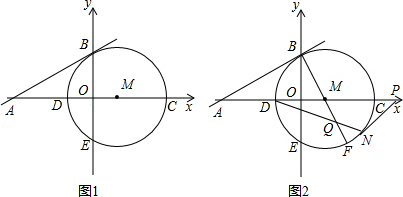
 如图1,已知直线:y=
如图1,已知直线:y=
| ||
| 3 |
| 3 |
 |
| CF |
 |
| CF |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 4 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 4 |
| 27 |
| 22 |
| 3 |

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com