Question

19．用正方形硬纸板做三棱柱盒子，每个盒子由3个矩形侧面和2个正三角形底面组成，硬纸板以如图两种方法裁剪（裁剪后边角料不再利用）

A方法：剪6个侧面； 
B方法：剪4个侧面和5个底面．
现有38张硬纸板，裁剪时x张用A方法，其余用B方法．
（1）用x的代数式分别表示裁剪出的侧面和底面的个数；
（2）若裁剪出的侧面和底面恰好全部用完，问能做多少个盒子？

Answer 1

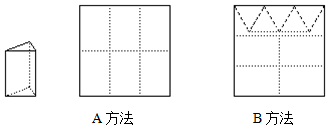
分析 （1）由x张用A方法，就有（38-x）张用B方法，就可以分别表示出侧面个数和底面个数；
（2）由侧面个数和底面个数比为3：2建立方程求出x的值，求出侧面的总数就可以求出结论．

解答 解：（1）∵裁剪时x张用A方法，
∴裁剪时（38-x）张用B方法．
∴侧面的个数为：6x+4（38-x）=（2x+152）个，
底面的个数为：5（38-x）=（180-5x）个；

（2）由题意，得（2x+152）：（190-5x）=3：2，
解得：x=14，
∴盒子的个数为：$\frac{2×14+152}{3}$=60．
答：裁剪出的侧面和底面恰好全部用完，能做60个盒子．

点评 本题考查了列一元一次方程解实际问题的运用，一元一次方程的解法的运用，列代数式的运用以及分式方程的应用，解答时根据裁剪出的侧面和底面个数相等建立方程是关键．