
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:分析 首先根据开口方向确定a的取值范围,根据对称轴的位置确定b的取值范围,根据抛物线与y轴的交点确定c的取值范围,可判断①;令x=-1,可判断②;根据图象和x=2的函数值即可确定4a+2b+c的取值范围,可判断③;利用当x=1时,y最大,即a+b+c最大,故a+b+c>an2+bn+c,可判断④.
解答 解:∵抛物线开口朝下,
∴a<0,
∵对称轴x=1=-$\frac{b}{2a}$,
∴b>0,
∵抛物线与y轴的交点在x轴的上方,
∴c>0,
∴abc<0,故①错误;
根据图象知道当x=-1时,y=a-b+c<0,
∴a+c<b,故②正确;
根据图象知道当x=2时,y=4a+2b+c>0,故③正确;
∵当x=1时,y最大,即a+b+c最大,故a+b+c>an2+bn+c,即a+b>n(an+b),(n为实数且n≠1),故④正确;
综上所述,②③④正确.
故答案为:②③④.
点评 此题主要考查了图象与二次函数系数之间的关系,二次函数与方程之间的转换,关键是会利用特殊值代入法求得特殊的式子,如:y=a+b+c,然后根据图象判断其值.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 4.5 | C. | 5 | D. | 5.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
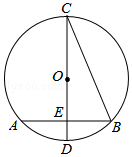 如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC,若AB=2$\sqrt{2}$cm,∠BCD=22°30′,则⊙O的半径为( )
如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,连接BC,若AB=2$\sqrt{2}$cm,∠BCD=22°30′,则⊙O的半径为( )| A. | 4cm | B. | 3cm | C. | 2cm | D. | 1cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com