
分析 (1)根据已知的式子中被除数与除数中x的次数的关系即可求解;
(2)根据已知的式子中被除数与除数中x的次数的关系即可直接求解;
(3)①把所求的式子作为已知中式子的商,乘以除数(2-1),即可求得被除数;
②设S=1+(-2)+(-2)2+(-2)3+…+(-2)2014=1-2+22-23+24+…+22014,则2S=2-22+23-24+25+…+22015,两个式子相加即可求得S的值.
解答 解:(1)m=2014+1=2015;
(2)(xn-1)÷(x-1)=xn-1+xn-2+xn-3+…+x+1;
(3)①1+2+22+…+22014=(22015-1)÷(2-1)=22015-1;
②设S=1+(-2)+(-2)2+(-2)3+…+(-2)2014=1-2+22-23+24+…+22014,
则2S=2-22+23-24+25+…+22015,
两式相加得:3S=1+22015,
则S=$\frac{1+{2}^{2015}}{3}$.
点评 本题考查了整式的除法,正确理解被除数、除数以及商的关系是解题的关键.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
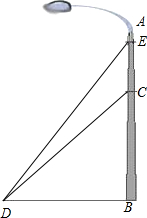 一灯柱AB被一钢缆CD固定,CD与地面成45°夹角,且BD=5m,现再在C点上方2m处加固另一根钢缆ED,那么钢缆ED的长度为多少?(结果保留根号)
一灯柱AB被一钢缆CD固定,CD与地面成45°夹角,且BD=5m,现再在C点上方2m处加固另一根钢缆ED,那么钢缆ED的长度为多少?(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
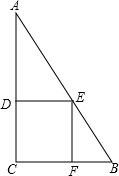 如图,在Rt△ABC中,AC=h cm,四边形DEFC是矩形,且点D、E、F在△ABC的边上,设AD=x cm,CF=$\frac{20x}{h}$cm,矩形DEFC的面积为y cm2.
如图,在Rt△ABC中,AC=h cm,四边形DEFC是矩形,且点D、E、F在△ABC的边上,设AD=x cm,CF=$\frac{20x}{h}$cm,矩形DEFC的面积为y cm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com