解:(1)∵AE=BF=CP=t,
∴AP=5-t,
在?ABCD中,AD=BC=AC=5,AB=EF=CD=6,
∵PE∥CD,
∴△APE∽△ACD,
∴
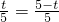
,
∴t=2.5,
此时点P、E分别为AC、AD的中点,
∴PE=

=

=3cm;
(2)△PEF是等腰三角形
证明:在?ABCD中,AD=BC=AC,AB=EF=CD,
∴∠CAB=∠CBA,

∵AB∥EF,
∴∠CQF=∠CAB,∠CFQ=∠CBA,
∴∠CFQ=∠CQF,
∴CF=CQ,
∴AQ=BF=AE,
∴AP=CQ=CF,
∵AD∥BC,
∴∠PAE=∠FCP,
∴△PAE≌△FCP,
∴PE=PF;
(3)(ⅰ)在上述运动过程中,五边形ABFPE的面积④(填序号)
(ⅱ)∵△AQE∽△ACD,
∴
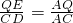
,
∴
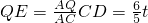
过点P作PH⊥EF于点H,过点C作CG⊥AB于点G,
∴△PQH∽△CAG,
∴

,
∴PH=
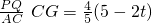
∴y=

∴当
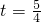
时,y
最大=

,
∴0<y≤

.
分析:(1)根据题意推出AP的长度,然后推出△APE∽△ACD,根据对应边成比例,即可推出t的值,推出点P、E分别为AC、AD的中点,即可推出EF的长度;
(2)根据题意推出∠CFQ=∠CQF,既而推出CF=CQ,因此AQ=BF=AE,AP=CQ=CF,从而推出△PAE≌△FCP,因此PE=PF,即△PEF是等腰三角形;
(3)①根据题意,即可推出不变,②过点P作PH⊥EF于点H,过点C作CG⊥AB于点G,通过求证△AQE∽△ACD,△PQH∽△CAG,即可推出QE,PH关于t的表达式,即可推出y关于t的解析式,根据二次函数的最值即可推出y的取值范围.
点评:本题主要考查相似三角形的判定和性质、全等三角形的判定和性质、等腰三角形的判定、平行四边形的性质,关键在于熟练地运用各个性质求证相关的三角形相似.

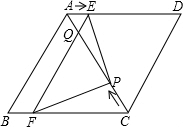 (1)当t为何值时,PE∥CD?并求出此时PE的长;
(1)当t为何值时,PE∥CD?并求出此时PE的长;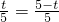 ,
, =
= =3cm;
=3cm;
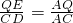 ,
,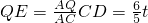
 ,
,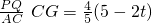

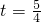 时,y最大=
时,y最大= ,
, .
.

 如图,在?ABCD中,对角线AC、BD相交于点O,AB=
如图,在?ABCD中,对角线AC、BD相交于点O,AB=
 (2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.
(2011•犍为县模拟)甲题:已知关于x的一元二次方程x2=2(1-m)x-m2的两实数根为x1,x2.