Question

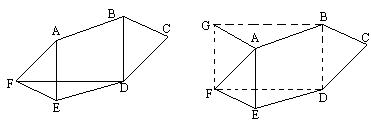
如图，六边形ABCDEF中，AB∥DE，AF∥CD，BC∥FE，AB＝DE，BC＝FE．对角线FD⊥BD，FD＝24cm，BD＝18cm．你能求出六边形ABCDEF的面积是多少平方厘米吗？为了解决这个问题，王强同学运用平移的知识进行如下操作：如图将△DEF平移到△BAG的位置；将△BCD平移到△GAF的位置．于是他很快说出它的面积．请问：①王强同学两次平移三角形的目的是________；②六边形ABCDEF的面积是________cm²．

Answer 1

答案：
解析：

把求不规则的六边形ABCDEF的面积转化为求长方形BDFG的面积,432 　　本题初看似乎无法求解，经仔细观察，题中彼此平行且相等的线段有三组AB∥DE、AF∥CD、BC∥FE，又知AB＝DE，BC＝FE，FD⊥BD，于是可以大胆设想：将六边形ABCDEF剪成△BCD、△DEF和四边形AFDB，并将△DEF平移到△BAG的位置；将△BCD平移到△GAF的位置，则拼成的图形是一个长方形BDFG． 因此六边形ABCDEF的面积等于长方形BDFG的面积，即24×18＝432(cm2)．