
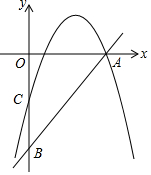
 如图,直线y=2x-10分别与x轴,y轴交于点A,B,点C为OB的中点,抛物线y=-x2+bx+c经过A,C两点.
如图,直线y=2x-10分别与x轴,y轴交于点A,B,点C为OB的中点,抛物线y=-x2+bx+c经过A,C两点.分析 (1)由直线解析式求出A、B坐标,然后得出C点坐标,再用待定系数法求出抛物线解析式;
(2)①过D作DE∥y轴交AB于E,则S△ABD=S△BDE+S△ADE=,设出D点的横标,纵坐标用横坐标表示,同时表示出E点坐标,从而得出△ABD的面积表达式,再根据△ABD的面积为$\frac{45}{2}$,列出方程解之即可;
②分两种情况:第一种,D为直角顶点;第二种,P为直角顶点.对于第一种情况,可以验证抛物线的顶点与D、A一起刚好构成直角三角形,即P点就是抛物线的顶点;对于第二种情况,过点P作GH∥x轴,DG⊥GH于G,AH⊥GH于H,由△DGP∽△PHA列出相似比例关系求解.
解答 解:(1)当y=0时,2x-10=0,解得x=5,则A(5,0),
当x=0时,y=2x-10=-10,则B(0,-10)
∵点C为OB的中点,
∴C(0,-5),
把A(5,0),C(0,-5)代入y=-x2+bx+c得$\left\{\begin{array}{l}{-25+5b+c=0}\\{c=-5}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=6}\\{c=-5}\end{array}\right.$,
∴抛物线解析式为y=-x2+6x-5;
(2)①过D作DE∥y轴交AB于E,如图,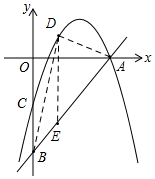
设D(x,-x2+6x-5),则E(x,2x-10),
∵S△ABD=S△BDE+S△ADE=$\frac{1}{2}$×5×DE=$\frac{5}{2}$(-x2+6x-5-2x+10)
∴$\frac{5}{2}$(-x2+6x-5-2x+10)=$\frac{45}{2}$,
整理得x2-4x+4=0,解得x1=x2=2,
∴D(2,3);
②∵抛物线解析式为y=-x2+6x-5,
∴抛物线的顶点为M(3,4),
∴MD=$\sqrt{2}$,AD=3$\sqrt{2}$,AM=2$\sqrt{5}$,
∴MD2+AD2=AM2,
∴MD⊥AD,
若D为直角顶点,则P与M点重合,即P(3,4),如图,
此时P点到抛物线对称轴的距离为0;
若P为直角顶点,如图,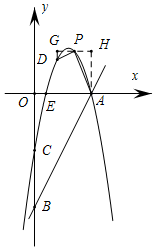
过点P作GH∥x轴,DG⊥GH于G,AH⊥GH于H,
∵∠APD=90°,
∴△DGP∽△PHA,
∴$\frac{DG}{GP}=\frac{PH}{AH}$,
设P(t,-t2+6t-5),则:
GP=t-2,DG=-t2+6t-5-3,PH=5-t,AH=-t2+6t-5,
∴$\frac{-{t}^{2}+6t-5-3}{t-2}=\frac{5-t}{-{t}^{2}+6t-5}$,
∴$\frac{-(t-2)(t-4)}{t-2}=\frac{t-5}{(t-1)(t-5)}$,
∴$\frac{4-t}{1}=\frac{1}{t-1}$,
∴t2-5t+5=0,
∴t=$\frac{5±\sqrt{5}}{2}$,
∴P点坐标为($\frac{5-\sqrt{5}}{2}$,$\frac{5-\sqrt{5}}{2}$)或($\frac{5+\sqrt{5}}{2}$,$\frac{5+\sqrt{5}}{2}$);
若P点坐标为($\frac{5-\sqrt{5}}{2}$,$\frac{5-\sqrt{5}}{2}$),则P点到抛物线对称轴的距离为$\frac{1+\sqrt{5}}{2}$,
若P点坐标为($\frac{5+\sqrt{5}}{2}$,$\frac{5+\sqrt{5}}{2}$),则P点到抛物线对称轴的距离为$\frac{\sqrt{5}-1}{2}$.
点评 本题是二次函数综合题,主要考查了一次函数图象上坐标点的特征,待定系数法求二次函数解析式,三角形面积的铅垂高表示法,解一元二次方程,勾股定理,相似三角形的判定与性质等重要知识点,综合性强,难度较大.对于最后一问,要注意两点:第一,分类讨论;第二,对于直角三角形这个条件的利用,很多同学可能会选择分别表示出三条边长,用勾股定理列出复杂的方程进行计算,这种想法虽然理论上可行,但计算量大,如果方程太复杂,可能会解不出来,大多数情况下,合理的做法是构造相似三角形,利用相似比例关系进行求解,这样做的好处在于使计算量大大降低.“能用相似就不用勾股”,这一原则在很多情况下是适用的.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一、二象限 | B. | 第一、三象限 | C. | 第二、四象限 | D. | 第三、四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “射击运动员射击一次,命中靶心”是必然事件 | |
| B. | 不可能事件发生的概率为0 | |
| C. | 随机事件发生的概率为$\frac{1}{2}$ | |
| D. | 投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com