
如图,在矩形ABCD中,点O在对角线AC上,以 OA长为半径的⊙O与AD、AC分别交于点E、F,且∠ACB=∠DCE.
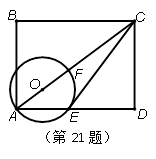
(1)求证:CE是⊙O的切线;
(2)若tan∠ACB=![]() ,AE=7,求⊙O的直径.
,AE=7,求⊙O的直径.
(1)证明略
(2)![]()
解析:(1)证明:连接OE,
∵ 四边形ABCD是矩形,
∴ AD∥BC,∠D=90°.
∴ ∠3=∠1,∠2+∠5=90°. …………………………… 1分
又 OA=OE,∴ ∠3=∠4.
∵ ∠1=∠2,
∴ ∠4=∠2. …………………………………………… 2分
∴ ∠4+∠5=90°,即∠OEC=90°.
∴ OE⊥EC.
∴ CE是⊙O的切线. ……………………………………… 3分
(2)解:连接EF,

∵ AF是直径,∴∠AEF=90°.
∵ ∠ACB=∠3,
∴ tan∠3=tan∠ACB=![]() .………………………………………… 4分
.………………………………………… 4分
在RtΔAEF中,∵ tan∠3=![]() ,∴ cos∠3=
,∴ cos∠3=![]() .
.
∴ AF=![]() =
=![]() . 即 ⊙O的直径等于
. 即 ⊙O的直径等于![]() . ………………… 5分
. ………………… 5分


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:初中数学 来源: 题型:
 如图,在矩形ABCD中,AB=4cm,BC=8cm,点P从点A出发以1cm/s的速度向点B运动,点Q从点B出发以2cm/s的速度向点C运动,设经过的时间为xs,△PBQ的面积为ycm2,则下列图象能反映y与x之间的函数关系的是( )
如图,在矩形ABCD中,AB=4cm,BC=8cm,点P从点A出发以1cm/s的速度向点B运动,点Q从点B出发以2cm/s的速度向点C运动,设经过的时间为xs,△PBQ的面积为ycm2,则下列图象能反映y与x之间的函数关系的是( )A、 | B、 | C、 | D、 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 .
.| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 动过程中,Q点停留了1s,图②是P、Q两点在折线AB-BC-CD上相距的路程S(cm)与时间t(s)之间的函数关系图象.
动过程中,Q点停留了1s,图②是P、Q两点在折线AB-BC-CD上相距的路程S(cm)与时间t(s)之间的函数关系图象.查看答案和解析>>
科目:初中数学 来源: 题型:
 DE,EF与AB交于点F,设CE=x,BF=y.
DE,EF与AB交于点F,设CE=x,BF=y.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com