
【题目】在平面直角坐标系中,点A的坐标为(0,3),点B和点D的坐标分别为(m,0),(n,4),且m>0,四边形ABCD是矩形.
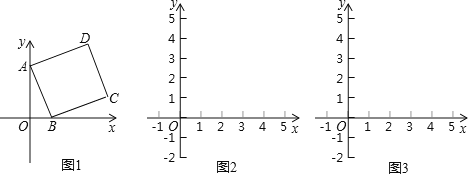
(1)如图1,当四边形ABCD为正方形时,求m,n的值;
(2)在图2中,画出矩形ABCD,简要说明点C,D的位置是如何确定的,并直接用含m的代数式表示点C的坐标;
(3)探究:当m为何值时,矩形ABCD的对角线AC的长度最短.
【答案】(1)m=1,n=3;(2)C(m+![]() ,1);(3)当m=
,1);(3)当m=![]() 时,矩形ABCD的对角线AC的长最短为4.
时,矩形ABCD的对角线AC的长最短为4.
【解析】
试题分析:(1)先判断出∠ADE=∠BAO,即可判断出△ABO≌△ADE,得出DE=OA=3,AE=OB,即可求出m;
(2)先根据垂直的作法即可画出图形,判断出△ADE≌△CBF,得出CF=1,再判断出△AOB∽△DEA,即可得出OB=![]() ,即可得出结论;
,即可得出结论;
(3)先判断出BD⊥x轴时,求出AC的最小值,再求出DM=2,最后用勾股定理求出AE即可得出m.
试题解析:(1)如图1,过点D作DE⊥y轴于E,
∴∠AED=∠AOB=90°,∴∠ADE+∠DAE=90°,
∵四边形ABCD是正方形,∴AD=AB,∠BAD=90°,
∴∠DAE+∠BAO=90°,∴∠ADE=∠BAO,
在△ABO和△ADE中,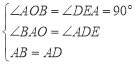 ,
,
∴△ABO≌△ADE,
∴DE=OA,AE=OB,
∵A(0,3),B(m,0),D(n,4),
∴OA=3,OB=m,OE=4,DE=n,∴n=3,
∴OE=OA+AE=OA+OB=3+m=4,∴m=1;
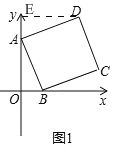
(2)画法:如图2,①过点A画AB的垂线l1,
过点B画AB的垂线l2,
②过点E(0,4),画y轴的垂线l3交l1于D,
③过点D画直线l1的垂线交直线l2于点C,
所以,四边形ABCD是所求作的图形,
过点C作CF⊥x轴于F,
∴∠CBF+∠BCF=90°,
∵四边形ABCD是矩形,∴AD=BC,∠ABC=∠BAD=90°,
∴∠ABO+∠CBF=90°,∴∠BCF=∠ABO,同理:∠ABO=∠DAE,
∴∠BCF=∠DAE,
在△ADE和△CBF中,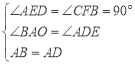 ,
,
∴△ADE≌△CBF,
∴DE=BF=n,AE=CF=1,
易证△AOB∽△DEA,∴![]() ,∴
,∴![]() ,∴n=
,∴n=![]() ,
,
∴OF=OB+BF=m+![]() ,∴C(m+
,∴C(m+![]() ,1);
,1);
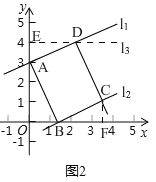
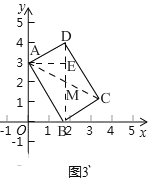
(3)如图3,由矩形的性质可知,BD=AC,
∴BD最小时,AC最小,
∵B(m,0),D(n,4),
∴当BD⊥x轴时,BD有最小值4,此时,m=n,
即:AC的最小值为4,
连接BD,AC交于点M,过点A作AE⊥BD于E,
由矩形的性质可知,DM=BM=![]() BD=2,
BD=2,
∵A(0,3),D(n,4),∴DE=1,∴EM=DM﹣DE=1,
在Rt△AEM中,根据勾股定理得,AE=![]() ,∴m=
,∴m=![]() ,即:
,即:
当m=![]() 时,矩形ABCD的对角线AC的长最短为4.
时,矩形ABCD的对角线AC的长最短为4.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某制衣店现购买蓝色.黑色两种布料共 138m,共花费 540 元.其中蓝色布料每米 3 元,黑色布料每米 5 元,两种布料各买多少米?设买蓝色布料 x 米,则依题意可列方程( )
A.3x 5138 x 540B.5x3138 x 540
C.3x5138x 540D.5x3138x 540
查看答案和解析>>
科目:初中数学 来源: 题型:
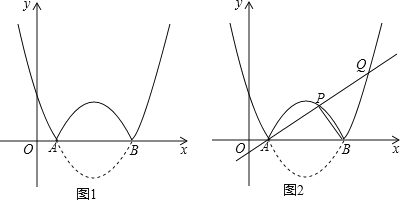
【题目】如图,抛物线l:y=![]() (x﹣h)2﹣2与x轴交于A,B两点(点A在点B的左侧),将抛物线ι在x轴下方部分沿轴翻折,x轴上方的图象保持不变,就组成了函数的图象.
(x﹣h)2﹣2与x轴交于A,B两点(点A在点B的左侧),将抛物线ι在x轴下方部分沿轴翻折,x轴上方的图象保持不变,就组成了函数的图象.
(1)若点A的坐标为(1,0).
①求抛物线l的表达式,并直接写出当x为何值时,函数的值y随x的增大而增大;
②如图2,若过A点的直线交函数的图象于另外两点P,Q,且S△ABQ=2S△ABP,求点P的坐标;
(2)当2<x<3时,若函数f的值随x的增大而增大,直接写出h的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市2013年底机动车的数量是2×106辆,2014年新增3×105辆,用科学记数法表示该市2014年底机动车的数量是( )
A.2.3×105辆
B.3.2×105辆
C.2.3×106辆
D.3.2×106辆
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平行四边形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() ,要使四边形
,要使四边形![]() 是正方形,还需添加一组条件。下面给出了四组条件:①
是正方形,还需添加一组条件。下面给出了四组条件:①![]() ,且
,且![]() ;②
;②![]() ,且
,且![]() ;③
;③![]() ,且
,且![]() ;④
;④![]() ,且
,且![]() ,其中正确的序号是 .
,其中正确的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com