解法1:如图将已知3个边长相等的正方形
以BE为轴进行翻折,连接BG′,FG′,设AB=a
则有∠EBG=∠EBG′
∠EBG+∠EBF=∠EBG′+∠EBF=∠FBG′
又BG′
2=a
2+(2a)
2=5a
2FG′
2=a
2+(2a)
2=5a
2,BF
2=a
2+(3a)
2=10a
2所以BG′
2+FG′
2=BF
2∠FBG′=45°
∠EBG+∠EBF=45°

解法2:如图连接BH,证△BHG∽△FHB
∠HBG=∠HFB,∠HGB=∠HBF得证.
∠EBF+∠EBG=∠BFA+∠AGB=∠BFA+∠HBF=45°.
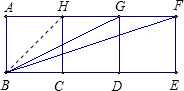
分析:此题有两种解法:解法1:如图将已知3个边长相等的正方形以BE为轴进行翻折,连接BG′,FG′设AB=a,再利用勾股定理即可解题.
解法2:如图连接BH,证△BHG∽△FHB,∠HBG=∠HFB,∠HGB=∠HBF得证.
点评:此题考查学生对相似三角形的判定与性质和勾股定理的理解和掌握,关于第二种解法,教师稍微提示,让学生自己再详细写下解题步骤.这样利用培养学生的独立学习能力.

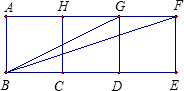 如图,已知3个边长相等的正方形相邻并排.求∠EBF+∠EBG.
如图,已知3个边长相等的正方形相邻并排.求∠EBF+∠EBG.



 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案