
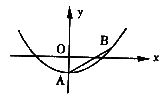
如图,有一横截面是抛物线的水渠,水渠管理员将一根长1.5m的标杆一端放在水渠底部的A点,另一端露出水面并靠在水渠边缘的B点,标杆有lm浸没在水中,露出水面的部分与水面成30°的夹角(标杆与抛物线的横截面在同一平面内),以水面所在直线为x轴,过点A垂直于水面的直线为y轴,建立如图所示的直角坐标系。求该水渠横截面抛物线的解析式(结果保留根号)
科目:初中数学 来源: 题型:
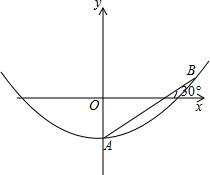 面在同一平面内).
面在同一平面内).| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
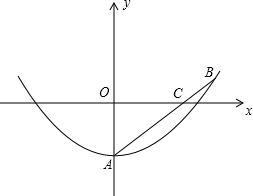
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2009-2010学年重庆市南开中学九年级(上)月考数学试卷(9月份)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com