
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:



查看答案和解析>>
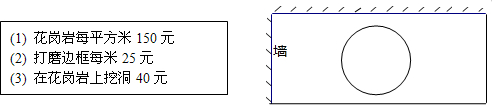
科目:初中数学 来源: 题型:
 所示),可制成高是4cm,容积是512cm3的一个无盖长方体纸盒.
所示),可制成高是4cm,容积是512cm3的一个无盖长方体纸盒.查看答案和解析>>
科目:初中数学 来源:鼎尖助学系列—同步练习(数学 八年级下册)、期末测试卷 题型:044
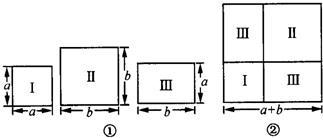
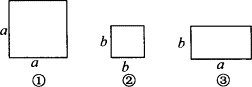
有若干张如图所示的正方形和长方形卡片.最多取出不超过五张,怎样将它们拼合,能组成一个边长为(a+b)的正方形?画出拼合后的图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
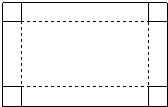
有一张长比宽多8cm的矩形纸板.如果在纸板的四个角处各剪去一个正方形(如图17所示),可制成高是4cm,容积是512cm3的一个无盖长方体纸盒.
⑴求矩形纸板的长和宽;
⑵在操作过程中,由于不小心,矩形纸板被剪掉一角,其直角边长分别为3cm和6cm.如果在剩余的纸板上先裁剪一个各边与原矩形纸板各边平行或重合的矩形,然后再按图的裁剪方式制作高仍是4cm的无盖长方体纸盒,那么你认为如何裁剪才能使制作的长方体纸盒的容积最大,请画出草图,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com