
 的平方根是( )
的平方根是( )
A.±12 B.12 C.± D.
D.
科目:初中数学 来源: 题型:
在进行二次根式简化时,我们有时会碰上如 ,
, ,
, 一样的式子,其实我
一样的式子,其实我 们还可将其进一步简化:
们还可将其进一步简化:
 =
= ;(一)
;(一)
 =
= =
= ;(二)
;(二)
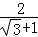 =
= =
= =
= ;(三)
;(三)
以上这种化简的步骤叫做分母有理化
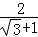 还可以用以下方法化简:
还可以用以下方法化简:
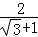 =
= =
= =
=
 ;(四)
;(四)
(1)化简 =__________
=__________ =__________
=__________
(2)请用不同的方法化简
 .
.
①参照(三)式得 =__________
=__________
②步骤(四)式得 =__________
=__________
(3)化简:
 +
+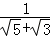 +
+ +…+
+…+ .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
“黄金1号”玉米种子的价格为5元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打6折,设购买种子数量为x千克,付款金额为y元,则y与x的函数关系的图象大致是( )
A. B.
B.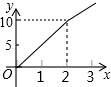 C.
C.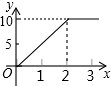 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
问题提出:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
问题探究:不妨假设能搭成m种不同的等腰三角形,为探究m与n之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
探究一:
(1)用3根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
此时,显然能搭成一种等腰三角形.所以,当n=3时,m=1
(2)用4根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形,所以,当n=4时,m=0
(3)用5根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形,所以,当n=5时,m=1
(4)用6根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和2根木棒,则能搭成一种等腰三角形,所以,当n=6时,m=1
综上所述,可得表①
| n | 3 | 4 | 5 | 6 |
| m | 1 | 0 | 1 | 1 |
探究二:
(1)用7根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?
(仿照上述探究方法,写出解答过程,并把结果填在表②中)
(2)分别用8根、9根、10根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三
角形?(只需把结果填在表②中)
| n | 7 | 8 | 9 | 10 |
| m |
你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究,…
解决问题:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
(设n分别等于4k﹣1、4k、4k+1、4k+2,其中k是整数,把结果填在表 ③中)
| n | 4k﹣1 | 4k | 4k+1 | 4k+2 |
| m |
问题应用:用2016根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(要求写出解答过程)
其中面积最大的等腰三角形每个腰用了__________根木棒.(只填结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,△ABC是等边三角形.P是∠ABC的平分线BD上一点,PE⊥AB于点E,线段BP的垂直平分线交BC于点F,垂足为点Q.若BF=2,则PE的长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知:在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD.图中的CE、BD有怎样的大小和位置关系?试证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com