Question

如图，O是直线AB上一点，OC为任一条射线，OD平分∠BOC，OE平分∠AOC。

（1）写出图中∠AOD与∠BOE的补角；
（2）试说明∠COD与∠COE具有怎样的数量关系。

Answer 1

（1）∠BOD与∠COD，∠EOA与∠EOC；（2）∠COD+∠COE=90°

解析试题分析：（1）根据补角、平角的定义结合角平分线的性质即可得到结果；
（2）由OD平分∠BOC，OE平分∠AOC，根据角平分线的性质结合平角的定义即可求得结果.
（1）∠AOD的补角为∠BOD与∠COD，∠BOE的补角为∠EOA与∠EOC；
（2）∵OD平分∠BOC，OE平分∠AOC
∴∠EOC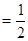∠AOC，∠COD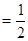∠BOC
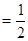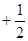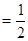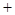∴∠COD+∠COE∠AOC∠BOC（∠AOC∠BOC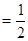）∠AOB=90°.
考点：本题考查的是补角的定义，平角的定义，角平分线的性质
点评：解答本题的关键是熟练掌握和为180°的两个角互为补角，邻补角的角平分线互相垂直.