若对任何实数a,关于x的方程x2-2ax-a+2b=0都有实数根,求实数b的取值范围.
解:∵关于x的方程x
2-2ax-a+2b=0都有实数根,
∴△=4a
2-4(-a+2b)=4a
2+4a-8b,
对任何实数a,有△=4a
2+4a-8b≥0,
所以△′≤0,即4
2-4×4×(-8b)≤0,
解得b≤
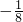
.
所以实数b的取值范围为b≤
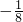
.
分析:先计算关于x的方程x
2-2ax-a+2b=0的△,把计算出的结果看作二次函数,开口向上,并且恒有△≥0,即函数图象不在x轴下方,因此得到△′≤0,解关于b的不等式即可.
点评:本题考查了一元二次方程ax
2+bx+c=0(a≠0,a,b,c为常数)根的判别式.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.同时考查了二次函数与一元二次方程的关系.

 .
. .
.
