
 已知:PA=
已知:PA= ,PB=4,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.如图,当∠APB=45°时,求AB及PD的长.
,PB=4,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.如图,当∠APB=45°时,求AB及PD的长.
 PA=
PA= ×
× =1,
=1, =
=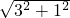 =
= ;
; AP=
AP= ×
× =2,
=2, =
= =2
=2 ,
, ,
, 、2
、2 .
. PA=
PA= ×
× =1,则BE=3,然后在Rt△AEB中,利用勾股定理可计算出AB=
=1,则BE=3,然后在Rt△AEB中,利用勾股定理可计算出AB= ;由于AD=AB,∠DAB=90°,则把△APD绕点A顺时针旋转90°得到△AFB,AD与AB重合,PA旋转到AF的位置,根据旋转的性质得到AP=AF,∠PAF=90°,PD=FB,则△APF为等腰直角三角形,得到∠APF=45°,PF=
;由于AD=AB,∠DAB=90°,则把△APD绕点A顺时针旋转90°得到△AFB,AD与AB重合,PA旋转到AF的位置,根据旋转的性质得到AP=AF,∠PAF=90°,PD=FB,则△APF为等腰直角三角形,得到∠APF=45°,PF= AP=
AP= ×
× =2,即有∠BPF=∠APB+∠APF=45°+45°=90°,然后在Rt△FBP中,根据勾股定理可计算出FB的长,即可得到PD的长.
=2,即有∠BPF=∠APB+∠APF=45°+45°=90°,然后在Rt△FBP中,根据勾股定理可计算出FB的长,即可得到PD的长.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
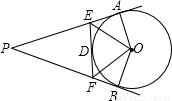
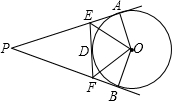 如图,已知:PA、PB、EF 分别切⊙O 于A、B、D,若PA=10cm,那么△PEF 周长是
如图,已知:PA、PB、EF 分别切⊙O 于A、B、D,若PA=10cm,那么△PEF 周长是查看答案和解析>>
科目:初中数学 来源:2010-2011学年江苏省连云港市灌云县鲁河中学九年级(上)期末复习数学试卷(1)(解析版) 题型:选择题
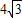
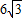
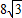
查看答案和解析>>
科目:初中数学 来源:2012年学大教育天津分公司教师专业水平考试初中数学试卷(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com