
����Ŀ��ij���г����ƻ�һ���������г�1400����ƽ��ÿ������200��������������ԭ��ʵ��ÿ����������ƻ�������г��룮�±���ij�ܵ����������������Ϊ����������Ϊ������

��1�����ݼ�¼�����ݿ�֪�ó������������������г�_______����
��2�����ܲ�������һ��Ȳ������ٵ�һ����������г�_______����
��3�����ݼ�¼�����ݿ�֪�ó�����ʵ���������г�_______����
��4���ó�ʵ��ÿ�ܼƼ������ƣ�ÿ����һ�����ɵ�50Ԫ���������������������ÿ�����⽱��20Ԫ��������һ����25Ԫ����ô�ó�������һ�ܵĹ����ܶ��Ƕ���Ԫ��
���𰸡���1��212����2��26����3��1410����4��70700��Ԫ
��������
���⣨1���ó��������������г�200+12=212����
��2����������һ��Ȳ������ٵ�һ����������г�16-��-10��=26����
��3���ó�����ʵ���������г���6-2-4+12-10+16-8��+200��7=1410����
��4����һ�ܵĹ����ܶ���200��7��50+��6-2-4+12-10+16-8������50+20��=70700Ԫ��
����������⣺��1��������Ϊ����������Ϊ���������������������г�200+12����
�ʸó��������������г�212����
��2������ͼʾ��������һ����216���������ٵ�һ����190��216-190=26����
�ʲ�������һ��Ȳ������ٵ�һ����������г�26����
��3����������֪��
6-2-4+12-10+16-8=10��200��7+10=1410����
�ʸó�����ʵ���������г�1410����
��4������ͼʾ���ܹ��˹����ܶ�=7��200��50+10��70=70700Ԫ��
�ʸó�������һ�ܵĹ����ܶ���70700Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���»��ľ���Ʒ�����������һ���ֱʣ�����Ϊÿ֧6Ԫ��Ϊ�˺������ۣ�������ǰ4�����л����۸�����ʱÿ֧��10ԪΪ��������10Ԫ�IJ��ּ�Ϊ��������10Ԫ�IJ��ּ�Ϊ�����ľߵ��¼��������øֱʵ��ۼ�������۳���������±���ʾ��
��1�� | ��2�� | ��3�� | ��4�� | |
ÿ֧�۸���Ա��۸�(Ԫ) | +1 | 0 | -1 | -2 |
�۳�֧��(֧) | 12 | 15 | 32 | 33 |
(1)��գ���������Ǯ�����ǵ�______�죬������______ԪǮ��
(2)���»��ľ���Ʒ��������������ֱָ�һ���˶���Ǯ��
(3)�»��ľ���Ʒ��������������Ǯȫ���������ֱָʣ�������Ϊÿ֧6ԪΪ�˴������ֱָʣ�ÿֻ�ֱʵ��ۼ���10Ԫ�Ļ����ϴ���ۣ����ι��������ֱָ�ȫ���۳����˶���Ǯ?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������߾���A����1��0����B��5��0����C��0�� ![]() �����㣮
�����㣮
��1���������ߵĽ���ʽ��
��2���������ߵĶԳ�������һ��P��ʹPA+PC��ֵ��С�����P�����ꣻ
��3����MΪx����һ���㣬�����������Ƿ����һ��N��ʹ��A��C��M��N�ĵ㹹�ɵ��ı���Ϊƽ���ı��Σ������ڣ����N�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ţ��ij��O��ʼ�ض�������ֱ�����У��涨�����е�·�̼�Ϊ�������������е�·�̼�Ϊ���������еĸ���·������Ϊ����λ�����ף���![]() .�ʣ�
.�ʣ�
��1����ţ����Ƿ�ص�������O��
��2����ţ�뿪������O��Զ�Ƕ������ף�
��3�������й����У����ÿ����1������һ��֥�飬����ţ�ɵõ�������֥�飿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������и���������Ӧ�Ĵ�������(�������ö��ŷֿ�):
+8��0.275��-|-2|��0��-1.04��-(-10)��![]() ��
��![]() ,
,![]() ,0.1.
,0.1.
������:�x ���y
����:�x ���y
��������: �x ���y
����: �x ���y
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ijУ�ۺ�ʵ���С���ͬѧ����������һ����DE�ĸ߶ȣ��������������ǰ��һ��¥ͤǰ��̨����A�㴦���������D������Ϊ30��������������ķ����ߵ�̨���µĵ�C�������������D������Ϊ60������֪A��ĸ߶�ABΪ2�ף�̨��AC���¶�Ϊ1��![]() ����AB��BC=1��
����AB��BC=1��![]() ������B��C��E������ͬһ��ֱ���ϣ�������������������DE�ĸ߶ȣ��������ĸ߶Ⱥ��Բ��ƣ���
������B��C��E������ͬһ��ֱ���ϣ�������������������DE�ĸ߶ȣ��������ĸ߶Ⱥ��Բ��ƣ���
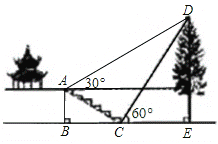
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��MN��ʾij��ˮ���̵�һ�����·�ߣ��ӵ�M����N������Ϊ��ƫ��30�����ڵ�M�ı�ƫ��60����������һ��A���Ե�AΪԲ�ģ���500��Ϊ�뾶��Բ������Ϊ��������ȡMN����һ��B�����BA�ķ���Ϊ��ƫ��75������֪MB=400�ף������ı䷽������ˮ·���Ƿ�ᴩ������������ͨ������˵�����ɣ����ο����ݣ� ![]() ��1.732��
��1.732��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ������A��BC��O���Ǿ���OABC(��OA��x���������ϣ���OC��y����������)�Ƶ�B��ʱ����ת�õ��ģ���O����x����������ϣ���B������Ϊ(1��3)��
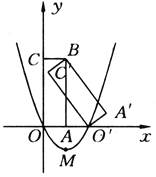
(1)������κ���y��ax2+bx+c��a��0)��ͼ��O��O�����㣬��ͼ��M��������Ϊ��l����������κ����Ľ���ʽ��
(2)��(1)������Ķ��κ���ͼ��Գ�����Ҳ࣬�Ƿ���ڵ�P��ʹ�á�POMΪֱ��������?�����ڣ������P������͡�POM��������������ڣ���˵�����ɣ�
(3)���C��O������ֱ�ߵĽ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��x2�ڵ�һ�����ھ�����������(�����ꡢ�����궼Ϊ�����ĵ�)����ΪA1��A2��A3��An����.��������y��x2��ֱ��L��y��x����ƽ�ƣ���һϵ�������ߣ������������������������ߵĶ���M1��M2��M3����Mn��������ֱ��L��y��x�ϣ������������ξ�����A1��A2��A3��An����.��M2014������Ϊ______________��
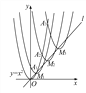
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com