
如图,一次函数y=2x﹣2的图象与x轴、y轴分别相交于B、A两点,与反比例函数 的图象在第一象限内的交点为M(3,m).
的图象在第一象限内的交点为M(3,m).
(1)求反比例函数的解析式;
(2)在x轴上是否存在点P,使AM⊥PM?若存在,求出点P的坐标;若不存在,说明理由.
(1)y=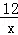 (2)存在.理由见解析
(2)存在.理由见解析
解析试题分析:(1)先把M(3,m)代入y=2x﹣2求出m,确定M点的坐标,然后利用待定系数法确定反比例函数解析式;
(2)先确定A点坐标为(0,﹣2),B点坐标为(1,0),再根据勾股定理计算出AB= ;根据M点坐标得到MC=4,BC=2,则利用勾股定理可计算出BM=2
;根据M点坐标得到MC=4,BC=2,则利用勾股定理可计算出BM=2 ,然后证明Rt△OBA∽Rt△MBP,利用相似比计算出BP,于是可确定P点坐标.
,然后证明Rt△OBA∽Rt△MBP,利用相似比计算出BP,于是可确定P点坐标.
解:(1)把M(3,m)代入y=2x﹣2得m=2×3﹣2=4,
∴M点坐标为(3,4),
把M(3,4)代入y=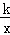 得k=3×4=12,
得k=3×4=12,
∴反比例函数的解析式为y=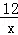 ;
;
(2)存在.
作MC⊥x轴于C,如图,
把x=0代入y=2x﹣2得y=﹣2;把y=0代入y=2x﹣2得2x﹣2=0,解得x=1,
∴A点坐标为(0,﹣2),B点坐标为(1,0),
∴OA=2,OB=1,
在Rt△OAB中,AB= =
=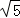 ,
,
∵M点坐标为(3,4),
∴MC=4,BC=3﹣1=2,
在Rt△MBC中,MB=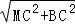 =2
=2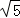 ,
,
∵MA⊥MB,
∴∠BMP=90°,
而∠OBA=∠MBP,
∴Rt△OBA∽Rt△MBP,
∴ =
=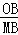 ,即
,即 =
= ,
,
∴BP=10,
∴OP=11,
∴点P的坐标为(11,0).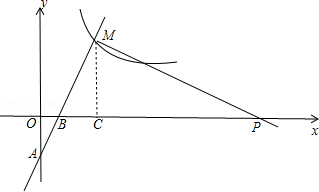
点评:本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征和待定系数法确定函数解析式;熟练运用勾股定理和相似比进行几何计算.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:解答题
已知图中的曲线是函数 (m为常数)图象的一支.
(m为常数)图象的一支.
(1)求常数m的取值范围;
(2)若该函数的图象与正比例函数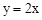 图象在第一象限的交点为A(2,n),求点A的坐标及反比例函数的解析式.
图象在第一象限的交点为A(2,n),求点A的坐标及反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,直线 与反比例函数
与反比例函数 的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(-1,m).
的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(-1,m).
(1)求反比例函数的解析式;
(2)若点P(n,1)是反比例函数图象上一点,过点P作PE⊥x轴于点E,延长EP交直线AB于点F,求△CEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系xOy中,△ABC的边AC在x轴上,边BC⊥x轴,双曲线 与边BC交于点D(4,m),与边AB交于点E(2,n).
与边BC交于点D(4,m),与边AB交于点E(2,n).
(1)求n关于m的函数关系式;
(2)若BD=2,tan∠BAC= ,求k的值和点B的坐标.
,求k的值和点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(2013年四川资阳9分)如图,已知直线l分别与x轴、y轴交于A,B两点,与双曲线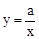 (a≠0,x>0)分别交于D、E两点.
(a≠0,x>0)分别交于D、E两点.
(1)若点D的坐标为(4,1),点E的坐标为(1,4):
①分别求出直线l与双曲线的解析式;
②若将直线l向下平移m(m>0)个单位,当m为何值时,直线l与双曲线有且只有一个交点?
(2)假设点A的坐标为(a,0),点B的坐标为(0,b),点D为线段AB的n等分点,请直接写出b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在平面直角坐标系中,点A(﹣3,4)关于y轴的对称点为点B,连接AB,反比例函数 (x>0)的图象经过点B,过点B作BC⊥x轴于点C,点P是该反比例函数图象上任意一点,过点P作PD⊥x轴于点D,点Q是线段AB上任意一点,连接OQ、CQ.
(x>0)的图象经过点B,过点B作BC⊥x轴于点C,点P是该反比例函数图象上任意一点,过点P作PD⊥x轴于点D,点Q是线段AB上任意一点,连接OQ、CQ.
(1)求k的值;
(2)判断△QOC与△POD的面积是否相等,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,点O为坐标原点,正方形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(2,2),反比例函数 (x>0,k≠0)的图像经过线段BC的中点D.
(x>0,k≠0)的图像经过线段BC的中点D.
(1)求k的值;
(2)若点P(x,y)在该反比例函数的图像上运动(不与点D重合),过点P作PR⊥y轴于点R,作PQ⊥BC所在直线于点Q,记四边形CQPR的面积为S,求S关于x的解析式并写出x的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
如图为一个表面分别标有:“A”、“B”、“C”、“D”、“E”、“F”六个字母的正方体的平面展开图如图,则与字母“B”所在的面字相对的面上标有字母“_________”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com