Question

用棱长为1cm的若干小正方体按如图所示的规律在地面上搭建若个几何体．图中每个几何体自上而下分别叫第一层，第二层…第n层（n为正整数），其中第一层摆放一个，第二层摆放4个，第三层摆放9个…，依次按规律摆放．（图片所示为第三个几何体）
（1）求搭建第4个几何体的小立方体的个数，第n个几何体第n层的个数及总数．
（2）画出第2，第3个几何体的三视图，并求出这两个几何体的所有露出部分（不含底面）的面积之和．
（3）为了美观，若将几何体的露出部分都涂上油漆（不含底面），已知喷涂1cm²需要油漆0.1g，求喷涂第n个几何体，共需要多少g油漆？（用含n的代数式表示）

Answer 1

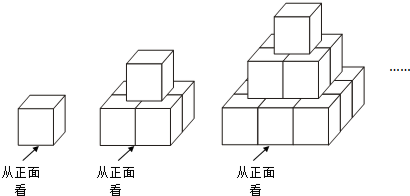
解：（1）搭建第4个几何体的小立方体的个数=1+4+9+16=30；第n个几何体第n层的个数为n²，其总数为1+2²+3²+4²+…+n²；

（2）第2个几何体的主视图为，左视图为，俯视图为；
第3个几何体的主视图为，左视图为，俯视图；
这两个几何体的所有露出部分（不含底面）的面积之和=4×3+4+4×6+9=49（cm²）；

（3）第n个几何体的所有露出部分（不含底面）的面积=4×（1+2+3+…+n）+n²=4×+n²=3n²+2n，
所以所需要的油漆量=（3n²+2n）×0.1=（0.3n²+0.2n）g．
分析：（1）观察得到每层向上的面都为正方形，即每层的个数都为平方数，则搭建第4个几何体的小立方体的个数=1+4+9+16；第n个几何体第n层的个数为n²，所以总数为1+2²+3²+4²+…+n²；
（2）根据三视图的画法分别画出两几何体得三视图；然后根据四个侧面和向上的面的小正方形的个数得到两个几何体的所有露出部分（不含底面）的面积之和；
（3）根据（2）中的方法得到第n个几何体的所有露出部分（不含底面）的面积=4×（1+2+3+…+n）+n²，化简后乘以0.1即可．
点评：此题主要考查了图形的变化类：通过特殊图象找到图象变化，归纳总结出规律，再利用规律解决问题．也考查了三视图．