
分析 (1)先根据AAS判定△AOE≌△BOC,得出OE=OC,再根据点C的坐标为(2,0),得到OC=2=OE,进而得到点E的坐标;
(2)先过点O作OM⊥AD于点M,作ON⊥BC于点N,根据△AOE≌△BOC,得到S△AOE=S△BOC,且AE=BC,再根据OM⊥AE,ON⊥BC,得出OM=ON,进而得到OD平分∠ADC;
(3)在DA上截取DP=DC,连接OP,根据SAS判定△OPD≌△OCD,再根据三角形外角性质以及三角形内角和定理,求得∠PAO=30°,进而得到∠OCB=60°.
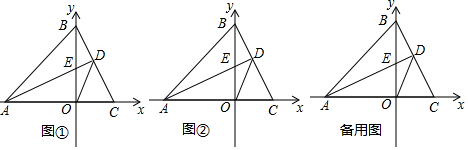
解答 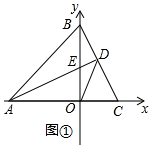 解:(1)如图①,∵AD⊥BC,BO⊥AO,
解:(1)如图①,∵AD⊥BC,BO⊥AO,
∴∠AOE=∠BDE,
又∵∠AEO=∠BED,
∴∠OAE=∠OBC,
∵A(-3,0),B(0,3),
∴OA=OB=3,
∴△AOE≌△BOC,
∴OE=OC,
又∵点C的坐标为(2,0),
∴OC=2=OE,
∴点E的坐标为(0,2);
(2)如图②,过点O作OM⊥AD于点M,作ON⊥BC于点N,
∵△AOE≌△BOC,
∴S△AOE=S△BOC,且AE=BC,
∵OM⊥AE,ON⊥BC,
∴OM=ON,
∴OD平分∠ADC;
(3)如所示,在DA上截取DP=DC,连接OP,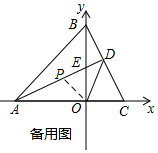
∵∠PDO=∠CDO,OP=OP,
∴△OPD≌△OCD,
∴OC=OP,∠OPD=∠OCD,
∵AD-CD=OC,
∴AD-DP=OP,即AP=OP,
∴∠PAO=∠POA,
∴∠OPD=∠PAO+∠POA=2∠PAO=∠OCB,
又∵∠PAO+∠OCD=90°,
∴3∠PAO=90°,
∴∠PAO=30°,
∴∠OCB=60°.
点评 本题属于三角形综合题,主要考查了全等三角形的判定与性质,角平分线的判定定理以及等腰直角三角形的性质的综合应用,解决问题的关键是作辅助线构造全等三角形,运用全等三角形的性质进行求解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两条直角边对应相等 | B. | 斜边和一直角边对应相等 | ||
| C. | 两个锐角对应相等 | D. | 斜边和一锐角对应相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$πxy的系数是$\frac{2}{3}$ | B. | 22xy2的次数是5 | ||
| C. | $\frac{-x+1}{3}$的常数项是1 | D. | 0是单项式 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4x2y与4y2x | B. | 2abc与2ab | C. | $-\frac{3}{a}$ 与-3a | D. | -x3y2与$\frac{1}{2}$y2x3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ( x+y ) | B. | (50x+60y) | C. | 110(x+y) | D. | (60x+50y) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com