Question

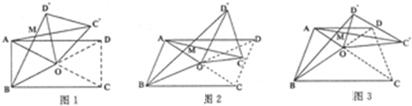
在四边形ABCD中，对角线AC、BD相交于点O，设锐角∠DOC=α，将△DOC按逆时针方向旋转得到△D′OC′（0°＜旋转角＜90°）连接AC′、BD′，AC′与BD′相交于点M．

（1）当四边形ABCD是矩形时，如图1，请猜想AC′与BD′的数量关系以及∠AMB与α的大小关系，并证明你的猜想；

（2）当四边形ABCD是平行四边形时，如图2，已知AC=BD，请猜想此时AC′与BD′的数量关系以及∠AMB与α的大小关系，并证明你的猜想；[来源:ZXXK]

（3）当四边形ABCD是等腰梯形时，如图3，AD∥BC，此时（1）AC′与BD′的数量关系是否成立？∠AMB与α的大小关系是否成立？不必证明，直接写出结论．

 

 

 

 

Answer 1

【答案】

解：（1）AC′=BD′，∠AMB=α，

证明：在矩形ABCD中，AC=BD，OA=OC=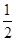AC，OB=O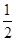D=BD，

∴OA=OC=OB=OD，

又∵OD=OD′，OC=OC′，

∴OB=OD′=OA=OC′，

∵∠D′OD=∠C′OC，

∴180°-∠D′OD=180°-∠C′OC，

∴∠BOD′=∠AOC′，

∴△BOD′≌△AOC′，

∴BD′=AC′，

∴∠OBD′=∠OAC′，

设BD^′与OA相交于点N，

∴∠BNO=∠ANM，

∴180°-∠OAC′-∠ANM=180°-∠OBD′-∠BNO，

即∠AMB=∠AOB=∠COD=α，

综上所述，BD′=AC′，∠AMB=α，

 

（2）AC′=kBD′，∠AMB=α，

证明：在平行四边形ABCD中，OB=OD，OA=OC，

又∵OD=OD′，OC=OC′，

∴OB：OA=OD′：C′，

∵∠D′OD=∠C′OC，

∴180°-∠D′OD=180°-∠C′OC，

∴∠BOD′=∠AOC′，

∴△BOD′∽△AOC′，

∴BD′：AC′=OB：OA=BD：AC，

∵AC=kBD，

∴AC′=kBD′，

∵△BOD′∽△AOC′，

设BD′与OA相交于点N，[来源:学+科+网Z+X+X+K]

∴∠BNO=∠ANM，

∴180°-∠OAC′-∠ANM=180°-∠OBD′-∠BNO，即∠AMB=∠AOB=α，

综上所述，AC′=kBD′，∠AMB=α，

[来源:ZXXK]

（3）AC′=BD′成立，∠AMB=α不成立．

【解析】略