Question

（2011•海南）如图，已知抛物线y=﹣x²+bx+9﹣b²（b为常数）经过坐标原点O，且与x轴交于另一点E．其顶点M在第一象限．
（1）求该抛物线所对应的函数关系式；
（2）设点A是该抛物线上位于x轴上方，且在其对称轴左侧的一个动点；过点A作x轴的平行线交该抛物线于另一点D，再作AB⊥x轴于点B．DE⊥x轴于点C．
①当线段AB、BC的长都是整数个单位长度时，求矩形ABCD的周长；
②求矩形ABCD的周长的最大值，并写出此时点A的坐标；
③当矩形ABCD的周长取得最大值时，它的面积是否也同时取得最大值？请判断井说明理由．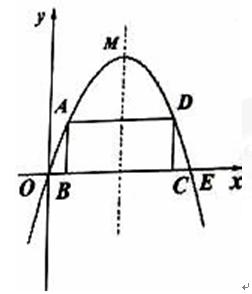

Answer 1

解：（1）由题意代入原点到二次函数式
则9﹣b²=0，
解得b=±3，
由题意抛物线的对称轴大于0，
，
所以b=3，
所以解析式为y=﹣x²+3x；
（2）根据两个三角形相似的条件，由于在△ECD中，∠ECD=60°，
若△BCP与△ECD相似，则△BCP中必有一个角为60°，
下面进行分类讨论：
①当P点直线CB的上方时，由于△PCB中，∠CBP＞90°或∠BCP＞90°，
∴△PCB为钝角三角形，
又∵△ECD为锐角三角形，
∴△ECD与△CPB不相似．
从而知在直线CB上方的抛物线上不存在点P使△CPB与△ECD相似；
②当P点在直线CB上时，点P与C点或B点重合，不能构成三角形，[来源:学§科§网]
∴在直线CB上不存在满足条件的P点；
③当P点在直线CB的下方时，若∠BCP=60°，则P点与E₁点重合，
此时，∠ECD=∠BCE₁，而，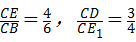
∴，
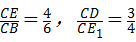∴△BCE与△ECD不相似，
若∠CBP=60°，则P点与A点重合，
根据抛物线的对称性，同理可证△BCA与△CED不相似，
若∠CPB=60°，假设抛物线上存在点P使△CPB与△ECD相似，
∴EF=sin60°×4=2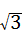，FD=1，
∴ED==，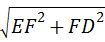
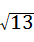∴当矩形ABCD的周长取得最大值时，它的面积能同时取得最大值．

解析