
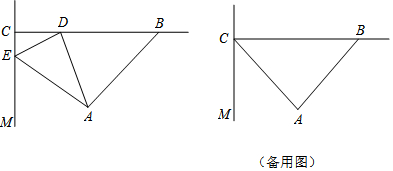
分析 (1)运用勾股定理直接求出;
(2)首先求出△ABD中BD边上的高,然后根据面积公式列出方程,求出BD的值,分两种情况分别求出t的值;
(3)假设△ABD≌△ACE,根据全等三角形的对应边相等得出BD=CE,分别用含t的代数式表示CE和BD,得到关于t的方程,从而求出t的值.
解答 解:(1)∵在△ABC中,AB=AC,∠BAC=90°,
∴2AB2=BC2,
∴AB=$\frac{BC}{\sqrt{2}}$=4$\sqrt{2}$cm;
(2)过A作AF⊥BC交BC于点F,则AF=$\frac{1}{2}$BC=4cm,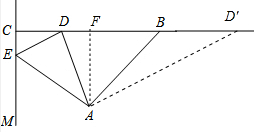
∵S△ABD=10cm2
∴AF×BD=20,
∴BD=5cm.
若D在B点右侧,则CD=3cm,t=1.5s;
若D在B点左侧,则CD=13cm,t=6.5s.
(3)动点E从点C沿射线CM方向运动$\frac{8}{3}$秒或当动点E从点C沿射线CM的反向延长线方向运动8秒时,△ABD≌△ACE.
理由如下:(说理过程简要说明即可)
①当E在射线CM上时,D必在CB上,则需BD=CE.
∵CE=t,BD=8-2t
∴t=8-2t,
∴t=$\frac{8}{3}$,
证明:在△ABD和△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠B=∠ACE=45°}\\{BD=CE}\end{array}\right.$,
∴△ABD≌△ACE(SAS).
②当E在CM的反向延长线上时,D必在CB延长线上,则需BD=CE.
∵CE=t,BD=2t-8,
∴t=2t-8,
∴t=8,
证明:在△ABD和△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠ABD=∠ACE=135°}\\{BD=CE}\end{array}\right.$,
∴△ABD≌△ACE(SAS).
∴动点E从点C沿射线CM方向运动$\frac{8}{3}$秒或当动点E从点C沿射线CM的反向延长线方向运动8秒时,△ABD≌△ACE.
点评 本题考查了等腰直角三角形的性质、全等三角形的判定和性质、三角形的面积等知识,解题的关键是学会用分类讨论的思想思考问题,学会构建方程,把问题掌握方程解决,属于中考压轴题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
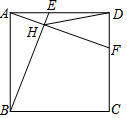 如图,正方形ABCD的边AD、CD上两个动点E,F,且满足AF=BE,BE交AF于点H.若正方形的边长为4,线段DH最大值为x,最小值为y,则$\sqrt{x}$-y的值是4-2$\sqrt{5}$.
如图,正方形ABCD的边AD、CD上两个动点E,F,且满足AF=BE,BE交AF于点H.若正方形的边长为4,线段DH最大值为x,最小值为y,则$\sqrt{x}$-y的值是4-2$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,AE⊥EF于点E,BF⊥EF于点F,连接AB交EF于点D.在线段AB上取一点C,使EB=EC=AC,若∠EBF=54°,则∠ABF=18°.
如图,AE⊥EF于点E,BF⊥EF于点F,连接AB交EF于点D.在线段AB上取一点C,使EB=EC=AC,若∠EBF=54°,则∠ABF=18°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
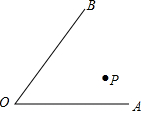 如图,∠AOB内有一点P
如图,∠AOB内有一点P查看答案和解析>>
科目:初中数学 来源: 题型:解答题
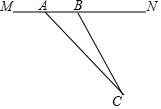 目前,我市正在积极创建文明城市,交通部门一再提醒司机:为了安全,请勿超速,并再进一步完善各类监测系统,如图,在某公路直线路段MN内限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据:$\sqrt{2}$=1.41,$\sqrt{3}$=1.73)
目前,我市正在积极创建文明城市,交通部门一再提醒司机:为了安全,请勿超速,并再进一步完善各类监测系统,如图,在某公路直线路段MN内限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据:$\sqrt{2}$=1.41,$\sqrt{3}$=1.73)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com