
若△ABC和△ADE均为等边三角形,M、N分别是BE、CD的中点
1.当△ADE绕A点旋转到如图①的位置时,求证:CD=BE,△AMN是等边三角形;
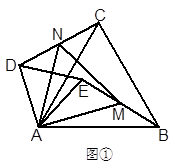
2.如图②,当∠EAB=30°,AB=12,AD=![]() 时,求AM的长.
时,求AM的长.
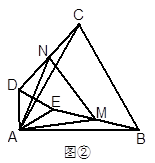
1.证明:∵△ABC和△ADE均为等边三角形,
∴AB=AC,AE=AD,∠BAC=∠EAD=60°.
∵∠BAE=∠BAC-∠EAC,∠DAC=∠EAD-∠EAC,
∴∠BAE=∠DAC.
∴△ABE≌△ACD.
∴CD=BE. ……………………………………………………………………1分
∠ABE=∠ACD.
∵M、N分别是BE、CD的中点,
即BM=![]() BE,CN=
BE,CN=![]() CD.
CD.
∴BM= CN.
又AB=AC,
∴△ABM≌△ACN.
∴AM=AN,∠MAB=∠NAC. ………………………………………………2分
∴∠NAM=∠NAC+∠CAM=∠MAB+∠CAM=∠CAB=60°.
∴△AMN是等边三角形.
2.解:作EF⊥AB于点F,
在Rt△AEF中,
∵∠EAB=30°,AE=AD=![]() ,
,
∴EF=![]() . …………………………………………………………………4分
. …………………………………………………………………4分
∵M是BE中点,
作MH⊥AB于点H,
∴MH∥EF,MH=![]() EF=
EF=![]() . ……………………………………………5分
. ……………………………………………5分
取AB中点P,连接MP,则MP∥AE,MP=![]() AE.
AE.
∴∠MPH=30°,MP=![]() .
.
∴在Rt△MPH中,PH=![]() .
.
∴AH=AP+PH=![]() . .………………………………………………………6分
. .………………………………………………………6分
在Rt△AMH中,AM=![]() . .…………………………7分
. .…………………………7分
解析:略


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•台州模拟)已知A、B、C、D点的坐标如图所示,E在线段AC的延长线上,若△ABC和△ADE相似,则E点的坐标是
(2012•台州模拟)已知A、B、C、D点的坐标如图所示,E在线段AC的延长线上,若△ABC和△ADE相似,则E点的坐标是| 16 |
| 13 |
| 15 |
| 13 |
| 16 |
| 13 |
| 15 |
| 13 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com