
分析 (1)设2012年底到2014年底该县手机拥有量的年平均增长率为x,根据增长率问题建立方程求出其解即可;
(2)设每年新增手机数量最多有a万部,则2015年底拥有的手机数量为(18×80%+a)万部,2016年底拥有的手机数量为[(18×80%+a)×80%+a]万部,根据要求到2016年底手机拥有量不会超过22.32万部建立不等式求出其解即可.
解答 解:(1)设2012年底到2014年底该县手机拥有量的年平均增长率为x,由题意,得
15(1+x)2=18,
解得:x1=0.2=20%,x2=-2.2(舍去)
答:2012年底到2014年底该县手机拥有量的年平均增长率为20%.
(2)设每年新增手机数量最多有a万部,则2015年底拥有的手机数量为(18×80%+a)万部,2016年底拥有的手机数量为[(18×80%+a)×80%+a]万部,由题意,得
(18×80%+a)×80%+a≤22.32,
解得:a≤6.
答:每年新增手机数量最多有6万部.
点评 本题考查了列一元二次方程和一元一次不等式组解实际问题的运用,解答本题时找到反应全题的等量关系或不相等关系建立方程和不等式是解答本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
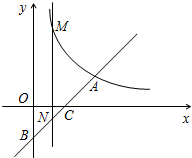 如图,在第一象限内,一次函数y=k1x-2的图象与反比例函数y=$\frac{k_2}{x}$的图象相交于点A(4,a),与y轴、x轴分别相交于B,C两点,且BC=CA.
如图,在第一象限内,一次函数y=k1x-2的图象与反比例函数y=$\frac{k_2}{x}$的图象相交于点A(4,a),与y轴、x轴分别相交于B,C两点,且BC=CA.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com