
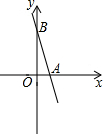 已知:如图,在平面直角坐标系xOy中,一次函数y=-4x+8的图象分别与x、y轴交于点A、B,点P在x轴的负半轴上,△ABP的面积为12.若一次函数y=kx+b的图象经过点P和点B,求这个一次函数y=kx+b表达式.
已知:如图,在平面直角坐标系xOy中,一次函数y=-4x+8的图象分别与x、y轴交于点A、B,点P在x轴的负半轴上,△ABP的面积为12.若一次函数y=kx+b的图象经过点P和点B,求这个一次函数y=kx+b表达式.| 1 |
| 2 |
|
|


科目:初中数学 来源: 题型:
| 1 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
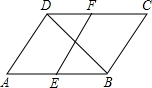 已知:如图,在平行四边形ABCD中,点E、F分别是AB、CD的中点.
已知:如图,在平行四边形ABCD中,点E、F分别是AB、CD的中点.查看答案和解析>>
科目:初中数学 来源: 题型:
| 每千克盈利(元) | 每天销售量(千克) | 每天盈利(元) | |
| 涨价前 | 10 | 500 | 5000 |
| 涨价后 | 6000 |
查看答案和解析>>
科目:初中数学 来源: 题型:
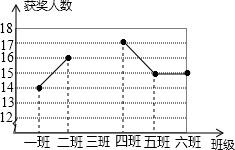 某中学组织网络安全知识竞赛活动,其中七年级6个班组每班参赛人数相同,学校对该年级的获奖人数进行统计,得到每班平均获奖15人,并制作成如图所示不完整的折线统计图.
某中学组织网络安全知识竞赛活动,其中七年级6个班组每班参赛人数相同,学校对该年级的获奖人数进行统计,得到每班平均获奖15人,并制作成如图所示不完整的折线统计图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com