
(本小题满分10分)
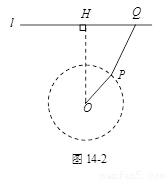
观察思考
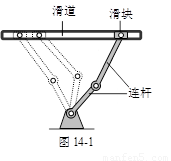
某种在同一平面进行传动的机械装置如图14-1,图14-2是它的示意图.其工作原理是:滑块Q在平直滑道l上可以左右滑动,在Q滑动的过程中,连杆PQ也随之运动,并且PQ带动连杆OP绕固定点O摆动.在摆动过程中,两连杆的接点P在以OP为半径的⊙O上运动.数学兴趣小组为进一步研究其中所蕴含的数学知识,过点O作OH ⊥l于点H,并测得OH = 4分米,PQ = 3分米,OP = 2分米.
解决问题
(1)点Q与点O间的最小距离是 分米;点Q与点O间的最大距离是 分米;点Q在l上滑到最左端的位置与滑到最右端位置间的距离是 分米.
(2)
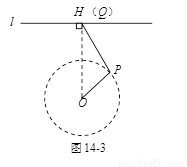
如图14-3,小明同学说:“当点Q滑动到点H的位置时,PQ与⊙O是相切的.”你认为他的判断对吗?为什么?
(3)①小丽同学发现:“当点P运动到OH上时,点P到l的距离最小.”事实上,还存在着点P到l距离最大的位置,此时,点P到l的距离是 分米;
②当OP绕点O左右摆动时,所扫过的区域为扇形,求这个扇形面积最大时圆心角的度数.
(1)4 5 6
(2)不对
(3)① 3
②120°
【解析】解:(1)4 5 6;
(2)不对.
∵OP = 2,PQ = 3,OQ = 4,且42≠32 + 22,即OQ2≠PQ2 + OP2,
∴OP与PQ不垂直.∴PQ与⊙O不相切.
(3)① 3;
②由①知,在⊙O上存在点P, 到l的距离为3,此时,OP将不能再向下转动,如图3.OP在绕点O左右摆动过程中所扫过的最大扇形就是
到l的距离为3,此时,OP将不能再向下转动,如图3.OP在绕点O左右摆动过程中所扫过的最大扇形就是 OP.
OP.

连结 P,交OH于点D.
P,交OH于点D.
∵PQ,
 均与l垂直,且PQ =
均与l垂直,且PQ =
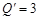 ,
,
∴四边形PQ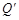
 是矩形.∴OH⊥P
是矩形.∴OH⊥P ,PD =
,PD = D.
D.
由OP = 2,OD = OH HD = 1,得∠DOP = 60°.
HD = 1,得∠DOP = 60°.
∴∠PO = 120°.
= 120°.
∴ 所求最大圆心角的度数为120°.


科目:初中数学 来源: 题型:
 .
.查看答案和解析>>
科目:初中数学 来源:2011年河北省中考模拟试卷数学卷 题型:解答题
(本小题满分10分)
如图,在平面直角坐标系中,直线L:y=-2x-8分别与x轴、y轴相交于A、B两点,点P(0,k)是y轴的负半轴上的一个动点,以P为圆心,3为半径作⊙P。
(1)连结PA,若PA=PB,试判断⊙P与X轴的位置关系,并说明理由;
(2)当K为何值时,以⊙P与直线L的两个交点和圆心P为顶点的三角形是正三角形?
查看答案和解析>>
科目:初中数学 来源:2011年四川省盐源县民族中学中考模拟试题数学卷 题型:解答题
(本小题满分10分)如图,在等腰梯形ABCD中,AD∥BC,AB=DC=5,AD=6,BC=12.动点P从D点出发沿DC以每秒1个单位的速度向终点C运动,动点Q从C点出发沿CB以每秒2个单位的速度向B点运动.两点同时出发,当P点到达C点时,Q点随之停止运动.
【小题1】(1)求梯形ABCD的面积;
【小题2】(2)当P点离开D点几秒后,PQ//AB;
【小题3】(3)当P、Q、C三点构成直角三角形时,求点P从点D运动的时间?
查看答案和解析>>
科目:初中数学 来源:2011-2012年河北省衡水市五校九年级第三次联考数学卷 题型:解答题
(本小题满分10分)如图,在平面直角坐标系中,点A、B、C、P的坐标分别为(0,1)、(-1,0)、(1,0)、(-1,-1)。
【小题1】(1)求经过A、B、C三点的抛物线的表达式;
【小题2】(2)以P为位似中心,将△ABC放大,使得放大后的△A1B1C1
与△OAB对应线段的比为3:1,请在右图网格中画出放大
后的△A1B1C1;(所画△A1B1C1与△ABC在点P同侧);
【小题3】(3)经过A1、B1、C1三点的抛物线能否由(1)中的抛物线平
移得到?请说明理由。
查看答案和解析>>
科目:初中数学 来源:2012届河南省商丘市九年级上学期期末考试数学卷 题型:解答题
(本小题满分10分)
在图1至图3中,直线MN与线段AB相交
于点O,∠1 = ∠2 = 45°.
【小题1】(1)如图1,若AO = OB,请写出AO与BD
的数量关系和位置关系;
【小题2】(2)将图1中的MN绕点O顺时针旋转得到
图2,其中AO = OB.
求证:AC = BD,AC ⊥ BD;
【小题3】(3)将图2中的OB拉长为AO的k倍得到
图3,求 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com