
如图(1),在平面直角坐标系中,AB⊥x轴于B,AC⊥y轴于C,点C(0,m),A(n,m),且(m-4)2+n2-8n=-16,过C点作∠ECF分别交线段AB、OB于E、F两点.
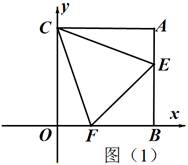
(1)求A点的坐标(3分);
(2)若OF+BE=AB,求证:CF=CE(4分)
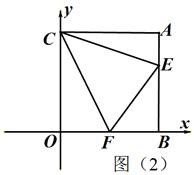
(3)如图(2),若∠ECF=45°,给出两个结论:OF+AE-EF的值不变;‚OF+AE+EF的值不变,其中有且只有一个结论正确,请你判断出正确的结论,并加以证明和求出其值(5分).
(1)(4,4);(2)证明见解析;(3)OF+AE-EF值不变,且OF+AE-EF=0.
【解析】
试题分析:(1)可将(m-4)2+n2-8n=-16,通过移项、因式分解变形为:(m-4)2+(n-4)2=0.结合图象可知m、n都大于0,由此可得m=n=4.
(2)因为OF+BE=AB,所以OF=AE,由(1)易得四边形COAB是正方形;所以由SAS得△ACE≌△OCF,从而可证CF=CE.
(3)因为AC=OC,可想到绕点C将△ACE顺时针旋转900,到△OCH位置,如图,可证△HCF≌△ECF得HF=EF,而HF=AE+OF,所以OF+AE-EF=0.
试题解析:
解:(1)∵(m-4)2+n2-8n=-16,
∴(m-4)2+(n-4)2=0.
∴m=4,n=4.
证明:∵AB⊥x轴,AC⊥y轴,A(4,4),
∴AB=AC=OC=OB,
∠ACO=∠COB=∠ABO=90°,
∴四边形COAB是正方形
∴∠A=90°
∵OF+BE=AB=BE+AE
∴AE=OF,
∴△COF≌△CAE
∴CF=CE.
(3)OF+AE-EF值不变,且OF+AE-EF=0.如图,
证明:在x轴负半轴上取点H,使OH=AE,
∵CO=CA ∠COH=∠CAE
∴△ACE≌△OCH
∴∠1=∠2
CH=CE,AE=OH
又∵∠EOF=45°
∴∠HCF=45°
∴△HCF≌△ECF
∴HF=EF
∴OF+AE=OF+OH=HF=EF
即OF+AE-EF=0.
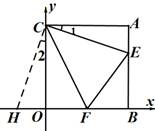
考点:1、正方形性质.2、三角形全等的判定.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
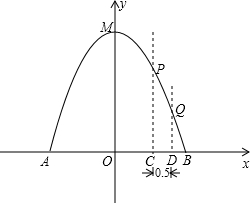 的体积和圆柱形桶的厚度忽略不计),以M点为顶点,抛物线对称轴为y轴,水平地面为x轴建立平面直角坐标系.
的体积和圆柱形桶的厚度忽略不计),以M点为顶点,抛物线对称轴为y轴,水平地面为x轴建立平面直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:
 水柱在与池中心的水平距离为1m处达到最高,高度为3m.
水柱在与池中心的水平距离为1m处达到最高,高度为3m.查看答案和解析>>
科目:初中数学 来源: 题型:

| 多面体 | 面数a | 展开图的顶点数b | 展开图的棱数c |
| 直三棱柱 | 5 | 10 | 14 |
| 四棱锥 | 5 5 |
8 | 12 |
| 立方体 | 6 6 |
14 14 |
19 19 |
查看答案和解析>>
科目:初中数学 来源:学习周报 数学 华师大八年级版 2009-2010学年 第13期 总第169期 华师大版 题型:044
工具阅读:
在平面上画两条原点重合、互相垂直且具有相同单位长度的数轴(如图),这就建立了平面直角坐标系.通常把其中水平的一条数轴叫做x轴或横轴,取向右为正方向;铅直的数轴叫做y轴或纵轴,取向上为正方向;两数轴的交点O叫做坐标原点.

问题探究:如图1,在6×6的方格纸中,给出如下三种变换:P变换,Q变换,R变换.

将图形F沿x轴向右平移1格得图形F1,称为作1次P变换;
将图形F沿y轴翻折得图形F2,称为作1次Q变换;
将图形F绕坐标原点顺时针旋转90°得图形F3,称为作1次R变换.
规定:PQ变换表示先作1次Q变换,再作1次P变换;QP变换表示先作1次P变换,再作1次Q变换;Rn变换表示作n次R变换.
解答下列问题:
(1)作R4变换相当于至少作________次Q变换;
(2)请在图2中画出图形F作R2011变换后得到的图形F4;

(3)PQ变换与QP变换是否是相同的变换?请在图3中画出PQ变换后得到的图形F5,在图4中画出QP变换后得到的图形F6.

查看答案和解析>>
科目:初中数学 来源:2011-2012学年重庆市南开中学九年级(上)第一次月考数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com