
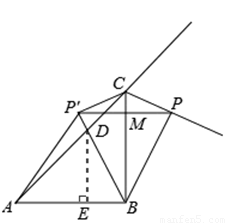
如图所示,在Rt△ABC中,AB=BC=4,∠ABC=90°,点P是△ABC的外角∠BCN的角平分线上一个动点,点P′是点P关于直线BC的对称点,连结PP′交BC于点M,BP′交AC于D,连结BP、AP′、CP′.
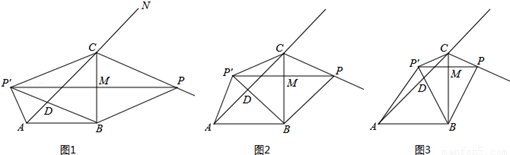
(1)若四边形BPCP′为菱形,求BM的长;
(2)若△BMP′∽△ABC,求BM的长;
(3)若△ABD为等腰三角形,求△ABD的面积.
解:(1)∵四边形BPCP′为菱形,而菱形的对角线互相垂直平分,
∴点M为BC的中点,∴BM=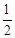 BC=
BC=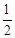 ×4=2。
×4=2。
(2)∵△ABC为等腰直角三角形,若△BMP′∽△ABC,
∴△BMP′必为等腰直角三角形,BM=MP′。
由对称轴可知,MP=MP′,PP′⊥BC,则△BMP为等腰直角三角形,
∴△BPP′为等腰直角三角形,BP′=BP。
∵∠CBP=45°,∠BCP=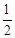 (180°﹣45°)=67.5°,
(180°﹣45°)=67.5°,
∴∠BPC=180°﹣∠CBP﹣∠BCP=180°﹣45°﹣67.5°=67.5°。
∴∠BPC=∠BCP。∴BP=BC=4。∴BP′=4。
在等腰直角三角形BMP′中,斜边BP′=4,∴BM=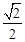 BP′=
BP′=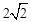 。
。
(3)△ABD为等腰三角形,有3种情形:
①若AD=BD,如题图②所示,此时△ABD为等腰直角三角形,斜边AB=4,
∴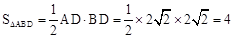 。
。
②若AD=AB,如答图①所示,
过点D作DE⊥AB于点E,则△ADE为等腰直角三角形,
∴DE=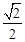 AD=
AD=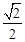 AB=
AB=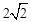 。
。
∴ ,
,
③若AB=BD,则点D与点C重合,可知此时点P、点P′、点M均与点C重合,
∴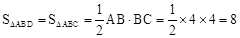 。
。
【解析】(1)由菱形的性质可知,点M为BC的中点,所以BM可求。
(2)△ABC为等腰直角三角形,若△BMP′∽△ABC,则△BMP′必为等腰直角三角形.证明△BMP′、△BMP、△BPP′均为等腰直角三角形,则BP=BP′;证明△BCP为等腰三角形,BP=BC,从而BP′=BC=4,进而求出BM的长度。
(3)△ABD为等腰三角形,有3种情形,分类讨论计算。


科目:初中数学 来源: 题型:
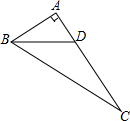 如图所示,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,则点D到BC的距离是( )
如图所示,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,则点D到BC的距离是( )| A、3 | B、4 | C、5 | D、6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 22、如图所示,在Rt△ABC中,∠C=90°,∠A=30°.作AB的中垂线l分别交AB、AC及BC的延长线于点D、E、F,连接BE. 求证:EF=2DE.
22、如图所示,在Rt△ABC中,∠C=90°,∠A=30°.作AB的中垂线l分别交AB、AC及BC的延长线于点D、E、F,连接BE. 求证:EF=2DE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com