
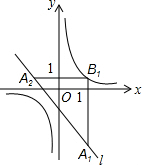
 如图,在平面直角坐标系xOy中,已知直线l:y=-x-1,双曲线y=$\frac{1}{x}$,在l上取一点A1,过A1作x轴的垂线交双曲线于点B1,过B1作y轴的垂线交l于点A2,请继续操作并探究:过A2作x轴的垂线交双曲线于点B2,过B2作y轴的垂线交l于点A3,…,这样依次得到l上的点A1,A2,A3,…,An,…记点An的横坐标为an,若a1=2,则a2=-$\frac{3}{2}$,a2016=-$\frac{1}{3}$;若要将上述操作无限次地进行下去,则a1不可能取的值是0或-1.
如图,在平面直角坐标系xOy中,已知直线l:y=-x-1,双曲线y=$\frac{1}{x}$,在l上取一点A1,过A1作x轴的垂线交双曲线于点B1,过B1作y轴的垂线交l于点A2,请继续操作并探究:过A2作x轴的垂线交双曲线于点B2,过B2作y轴的垂线交l于点A3,…,这样依次得到l上的点A1,A2,A3,…,An,…记点An的横坐标为an,若a1=2,则a2=-$\frac{3}{2}$,a2016=-$\frac{1}{3}$;若要将上述操作无限次地进行下去,则a1不可能取的值是0或-1. 分析 根据点的寻找规律,列出部分an值,可以发现规律“a3n+1=a1,a3n+2=-$\frac{{a}_{1}+1}{{a}_{1}}$,a3n=-$\frac{1}{{a}_{1}+1}$(n为正整数)”,根据该规律即可解决问题.
解答 解:当a1=2时,a2=-$\frac{3}{2}$,a3=-$\frac{1}{3}$,a4=2,…,
∴a3n+1=2,a3n+2=-$\frac{3}{2}$,a3n=-$\frac{1}{3}$(n为正整数).
∵2016=3×672,
∴a2016=-$\frac{1}{3}$.
观察,发现:a1,a2=-1-$\frac{1}{{a}_{1}}$=-$\frac{{a}_{1}+1}{{a}_{1}}$,a3=-1-$\frac{1}{{a}_{2}}$=-$\frac{1}{{a}_{1}+1}$,a4=-1-$\frac{1}{{a}_{3}}$=a1,…,
∴a3n+1=a1,a3n+2=-$\frac{{a}_{1}+1}{{a}_{1}}$,a3n=-$\frac{1}{{a}_{1}+1}$(n为正整数).
若要an有意义,只需a1≠0,a1+1≠0.
即a1≠0且a1≠-1.
故答案为:-$\frac{3}{2}$;-$\frac{1}{3}$;0或-1.
点评 本题考查了规律型的点的坐标以及反比例函数与一次函数的交点问题,解题的关键是发现规律“a3n+1=a1,a3n+2=-$\frac{{a}_{1}+1}{{a}_{1}}$,a3n=-$\frac{1}{{a}_{1}+1}$(n为正整数)”.本题属于中档题,难度不大,解决该题型题目时,罗列出部分an的值,根据an的变化找出规律是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
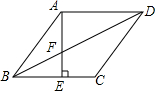 菱形ABCD中,AE⊥BC于E,交BD于F点,下列结论:
菱形ABCD中,AE⊥BC于E,交BD于F点,下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.16×108 | B. | 1.6×107 | C. | 1.6×108 | D. | 16×106 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com