2014
分析:由原方程可以得到x
2=x+2013,x=x
2-2013;然后根据一元二次方程解的定义知,x
12=x
1+2013,x
1=x
12-2013.由根与系数的关系知x
1+x
2=1,所以将其代入变形后的所求代数式求值.
解答:∵x
2-x-2013=0,
∴x
2=x+2013,x=x
2-2013,
又∵x
1,x
2是方程x
2-x-2013=0的两实数根,
∴x
1+x
2=1,
∴
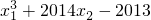
=x
1•

+2013x
2+x
2-2013,
=x
1•(x
1+2013)+2013x
2+x
2-2013,
=(x
1+2013)+2013x
1+2013x
2+x
2-2013,
=x
1+x
2+2013(x
1+x
2)+2013-2013,
=1+2013,
=2014,
故答案是:2014.
点评:本题考查了根与系数的关系、一元二次方程的解的定义.对所求代数式的变形是解答此题的难点.

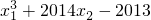 =________.
=________.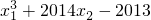
 +2013x2+x2-2013,
+2013x2+x2-2013,
