
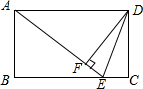
 如图,在矩形ABCD中,E是BC上一点,且AE=BC,DF⊥AE,垂足是F,连接DE.求证:(1)DF=AB;(2)DE是∠FDC的平分线.
如图,在矩形ABCD中,E是BC上一点,且AE=BC,DF⊥AE,垂足是F,连接DE.求证:(1)DF=AB;(2)DE是∠FDC的平分线. 分析 (1)由矩形的性质得出AD=BC,AB=DC,AD∥BC,∠B=∠C=90°,得出∠DAF=∠AEB,证出AD=AE,由AAS证明△ADF≌△EAB,即可得出结论;
(2)由HL证明Rt△DEF≌Rt△DEC,得出对应角相等∠EDF=∠EDC,即可得出结论.
解答 证明:(1)∵四边形ABCD是矩形,
∴AD=BC,AB=DC,AD∥BC,∠B=∠C=90°,
∴∠DAF=∠AEB,
∵AE=BC,
∴AD=AE,
∵DF⊥AE,
∴∠AFD=∠DFE=90°,
∴∠AFD=∠B,
在△ADF和△EAB中,$\left\{\begin{array}{l}{∠DAF=∠AEB}&{\;}\\{∠AFD=∠B}&{\;}\\{AD=AE}&{\;}\end{array}\right.$,
∴△ADF≌△EAB(AAS),
∴DF=AB;
(2)∵DF=AB,AB=DC,
∴DF=DC,
在Rt△DEF和Rt△DEC中,$\left\{\begin{array}{l}{DE=DE}\\{DF=DC}\end{array}\right.$,
∴Rt△DEF≌Rt△DEC(HL),
∴∠EDF=∠EDC,
∴DE是∠FDC的平分线.
点评 本题考查了矩形的性质、全等三角形的判定与性质;熟练掌握矩形的性质,证明三角形全等是解决问题的关键.


科目:初中数学 来源: 题型:解答题
| 月份 | 用水量(m3) | 收费(元) |
| 3 | 5 | 7.5 |
| 4 | 9 | 27 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 成本(元/个) | 售价 (元/个) | |
| A | 2 | 2.4 |
| B | 3 | 3.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1,2,3 | B. | 32,42,52 | C. | $\sqrt{2}$,$\sqrt{3}$,$\sqrt{5}$ | D. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
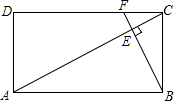 如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,$\frac{AD}{AB}$=$\frac{1}{2}$,△CEF的面积为S1,△AEB的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值等于$\frac{1}{16}$.
如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,$\frac{AD}{AB}$=$\frac{1}{2}$,△CEF的面积为S1,△AEB的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值等于$\frac{1}{16}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
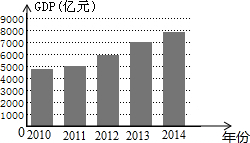 如图是表示某地区 2010~2014年生产总值(简称GDP,单位:亿元)的统计图,根据统计图所提供的信息,判断下列说法正确的是( )
如图是表示某地区 2010~2014年生产总值(简称GDP,单位:亿元)的统计图,根据统计图所提供的信息,判断下列说法正确的是( )| A. | 2012年该地区的GDP未达到5500亿元 | |
| B. | 2014年该地区的GDP比2012年翻一番 | |
| C. | 2012~2014年该地区每年GDP增长率相同 | |
| D. | 2012~2014年该地区的GDP逐年增长 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=1,b=1,c=2 | B. | a=$\sqrt{3}$,b=1,c=1 | C. | a=4,b=5,c=6 | D. | a=1,b=2,c=$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com