【题目】已知代数式x+2y的值是5，则代数式3x+6y+1的值是________．
科目：初中数学 来源： 题型：
【题目】倡导健康生活，推进全民健身，某社区要购进A，B两种型号的健身器材若干套，A，B两种型号健身器材的购买单价分别为每套310元，460元，且每种型号健身器材必须整套购买．
（1）若购买A，B两种型号的健身器材共50套，且恰好支出20000元，求A，B两种型号健身器材各购买多少套？
（2）若购买A，B两种型号的健身器材共50套，且支出不超过18000元，求A种型号健身器材至少要购买多少套？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如果向西走2018m记做 - 2018m，那么 + 2018m表示（ ）
A. 向东走2018m B. 向西走2018m C. 向南走2018m D. 向北走2018m
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将点A（﹣3，4）绕原点顺时针方向旋转180°后得到点B，则点B的坐标为（ ）
A.（3，﹣4）B.（﹣4，3）C.（﹣4，﹣3）D.（﹣3，﹣4）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知：
，点
……在射线ON上，点
……在射线OM上，△
、△
、△
……均为等边三角形，若
，则△
的边长为（ ）
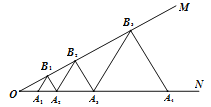
A. 6 B. 12 C. 32 D. 64
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】学习了三角形全等的判定方法（即“SAS”、“ASA”、“AAS”、“SSS”）和直角三角形全等的判定方法（即“HL”）后，我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究．
【初步思考】
我们不妨将问题用符号语言表示为：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，然后，对∠B进行分类，可分为“∠B是直角、钝角、锐角”三种情况进行探究．
【深入探究】
第一种情况：当∠B是直角时，△ABC≌△DEF．
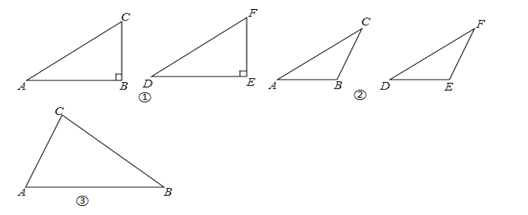
（1）如图①，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E=90°，根据______，可以知道Rt△ABC≌Rt△DEF．
第二种情况：当∠B是钝角时，△ABC≌△DEF．
（2）如图②，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是钝角，求证：△ABC≌△DEF．
第三种情况：当∠B是锐角时，△ABC和△DEF不一定全等．
（3）在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，请你用尺规在图③中作出△DEF，使△DEF和△ABC不全等．（不写作法，保留作图痕迹）
（4）∠B还要满足什么条件，就可以使△ABC≌△DEF？请直接写出结论：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，若______，则△ABC≌△DEF．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】点P1(x1,y1),点P2(x2,y2)是一次函数y=-3x-4图象上的两个点，且x1＞x2,则y1与y2的大小关系是（ ）
A.y1=y2B.y1＞y2C.y1＜y2D.y1＞y2＞0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
