
【题目】种植草莓大户张华有22吨草莓待售,现有两种销售渠道:一是运往省城成都直接批发给零售商;二是在遂宁本地市场零售. 经过调查分析,这两种销售渠道每天的销售量以及每吨所获纯利润见下表:
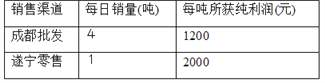
受客观因素和保质期影响,每天只能采用一种销售渠道并且必须在10日内将22吨草莓全部售出.
(1)设将![]() 吨草莓运往成都批发给零售商,其余在遂宁零售,请写出销售完22吨草莓所获纯利润
吨草莓运往成都批发给零售商,其余在遂宁零售,请写出销售完22吨草莓所获纯利润![]() (元)与
(元)与![]() (吨)之间的函数关系式;
(吨)之间的函数关系式;
(2)由于草莓必须在10日内售完,请你求出![]() 的取值范围;
的取值范围;
(3)怎样安排这22吨草莓的销售渠道,才能使所获纯利润最大?并求出最大纯利润.
【答案】(1)![]() (元)与
(元)与![]() (吨)之间的函数关系式是y=-800
(吨)之间的函数关系式是y=-800![]() +44000;
+44000;
(2)16≤![]() ≤22;
≤22;
(3)应安排16吨草莓运往成都批发给零售商,其余6吨草莓在遂宁零售,才能使所获纯利润最大,最大纯利润是31200元.
【解析】试题分析:(1)根据利润的关系,可得函数解析式;
(2)根据销售时间的关系,可得不等式组,根据解不等式组,可得答案;
(3)根据一次函数的性质,可得答案.
试题解析:(1)![]() (元)与
(元)与![]() (吨)之间的函数关系式是y=1200
(吨)之间的函数关系式是y=1200![]() +2000(22-
+2000(22-![]() ),即
),即![]() =-800
=-800![]() +44000;
+44000;
(2)根据题意,得: 
解得:16≤![]() ≤22;
≤22;
(3)∵一次函数![]() =-800
=-800![]() +44000中,
+44000中, ![]() =-800<0,
=-800<0,
∴![]() 随
随![]() 的增大而减小,
的增大而减小,
因此,当![]() =16时,
=16时, ![]() 的最大值=-800×16+44000=31200
的最大值=-800×16+44000=31200
∴应安排16吨草莓运往成都批发给零售商,其余6吨草莓在遂宁零售,才能使所获纯利润最大,最大纯利润是31200元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=2,O为AC中点,若点D在直线BC上运动,连接OE,则在点D运动过程中,线段OE的最小值是为( )
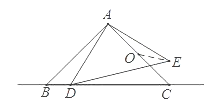
A.![]() B.
B.![]() C.1 D.
C.1 D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个一元二次方程:M:![]() N:
N:![]() ,其中
,其中![]() ,以下列四个结论中,错误的是( )
,以下列四个结论中,错误的是( )
A、如果方程M有两个不相等的实数根,那么方程N也有两个不相等的实数根;
B、如果方程M有两根符号相同,那么方程N的两根符号也相同;
C、如果5是方程M的一个根,那么![]() 是方程N的一个根;
是方程N的一个根;
D、如果方程M和方程N有一个相同的根,那么这个根必是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在△ABC中,BF、CF是角平分线,DE∥BC,分别交AB、AC于点D、E,DE经过点F.结论:①△BDF和△CEF都是等腰三角形;②DE=BD+CE; ③△ADE的周长=AB+AC;④BF=CF.其中正确的是______.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,AB=AC,D为BC的中点,以D为顶点作∠MDN=∠B.

(1)如图(1)当射线DN经过点A时,DM交AC边于点E,不添加辅助线,写出图中所有与△ADE相似的三角形.
(2)如图(2),将∠MDN绕点D沿逆时针方向旋转,DM,DN分别交线段AC,AB于E,F点(点E与点A不重合),不添加辅助线,写出图中所有的相似三角形,并证明你的结论.
(3)在图(2)中,若AB=AC=10,BC=12,当△DEF的面积等于△ABC的面积的![]() 时,求线段EF的长.
时,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,等腰△ABC中,AC=BC=![]() , ∠ACB=45,AO是BC边上的高,D为线段AO上一动点,以CD为一边在CD下方作等腰△CDE,使CD=CE且∠DCE=45,连结BE.
, ∠ACB=45,AO是BC边上的高,D为线段AO上一动点,以CD为一边在CD下方作等腰△CDE,使CD=CE且∠DCE=45,连结BE.
(1) 求证:△ACD≌△BCE;
(2) 如图2,在图1的基础上,延长BE至Q, P为BQ上一点,连结CP、CQ,若CP=CQ=5,求PQ的长.
(3) 连接OE,直接写出线段OE的最小值.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com