
分析 (1)解分式方程的步骤:①去分母;②求出整式方程的解;③检验;④得出结论,据此解答即可;
(2)首先应用乘方法,求出$\sqrt{x+2}$-$\sqrt{8-x}$=2的解有哪些;然后验根,判断出$\sqrt{x+2}$-$\sqrt{8-x}$=2的解是多少即可.
解答 解:(1)∵$\frac{3x-1}{{x}^{2}-1}$+1=$\frac{1}{x-1}$,
∴(3x-1)+(x2-1)=x+1,
整理,可得
x2+2x-3=0,
解得x=-3或x=1,
①当x=-3时,
左边=$\frac{3×(-3)-1}{{(-3)}^{2}-1}+1=-\frac{1}{4}$,
右边=$\frac{1}{-3-1}=-\frac{1}{4}$,
因为左边=右边,
所以x=-3是方程的解;
②当x=1时,
1-1=0,即分母为0,
所以x=1不是方程的解;
综上,可得方程$\frac{3x-1}{{x}^{2}-1}$+1=$\frac{1}{x-1}$的解是x=-3.
(2)∵$\sqrt{x+2}$-$\sqrt{8-x}$=2,
∴$\sqrt{x+2}$=2$+\sqrt{8-x}$,
${∴(\sqrt{x+2})}^{2}$=${(2+\sqrt{8-x})}^{2}$,
即x+2=12-x+4$\sqrt{8-x}$,
整理,可得2$\sqrt{8-x}$=x-5,
∴${(2\sqrt{8-x})}^{2}$=(x-5)2,
整理,可得x2-6x-7=0,
解得x=7或x=-1,
①把x=7代入原方程,可得
左边=$\sqrt{7+2}-\sqrt{8-7}=3-1=2$,
右边=2,
因为左边=右边,
所以x=7是方程$\sqrt{x+2}$-$\sqrt{8-x}$=2的解.
②把x=-1代入原方程,可得
左边=$\sqrt{-1+2}-\sqrt{8-(-1)}=1-3=-2$,
右边=2,
因为左边≠右边,
所以x=-1是方程$\sqrt{x+2}$-$\sqrt{8-x}$=2的解.
综上,可得方程$\sqrt{x+2}$-$\sqrt{8-x}$=2的解是x=7.
点评 (1)此题主要考查了分式方程的求解,解答此题的关键是要明确解分式方程的步骤:①去分母;②求出整式方程的解;③检验;④得出结论.
(2)此题还考查了无理方程的求解,要熟练掌握,解答此题的关键是要明确:①解无理方程常用的方法有:乘方法,配方法,因式分解法,设辅助元素法,利用比例性质法等.②用乘方法(即将方程两边各自乘同次方来消去方程中的根号)来解无理方程,往往会产生增根,应注意验根.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m≤14 | B. | m<14 | C. | m≥14 | D. | m>14 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,小虎站在自己家的A处,测得某信号塔CD的顶点C的俯角∠EAC为37°,底部D点的俯角∠EAD为50°,已知小虎家距地面的高度AB为60m.
如图,小虎站在自己家的A处,测得某信号塔CD的顶点C的俯角∠EAC为37°,底部D点的俯角∠EAD为50°,已知小虎家距地面的高度AB为60m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
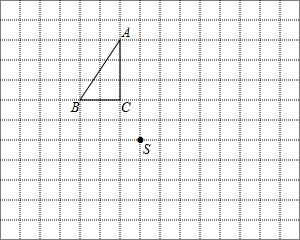 △ABC和点S都在正方形网格的格点上,每个小正方形的边长为1.
△ABC和点S都在正方形网格的格点上,每个小正方形的边长为1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com