
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
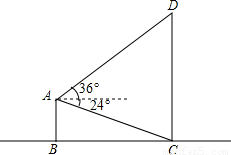
 (2012•龙川县二模)如图,AB与CD都是垂直于地面BC的建筑物.在建筑物AB的顶点A处测得建筑物CD的底端C的俯角为24°,测得顶端D的仰角为36°,若AC=200米,AD=300米,求建筑物CD的高度.(结果保留根号)
(2012•龙川县二模)如图,AB与CD都是垂直于地面BC的建筑物.在建筑物AB的顶点A处测得建筑物CD的底端C的俯角为24°,测得顶端D的仰角为36°,若AC=200米,AD=300米,求建筑物CD的高度.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:
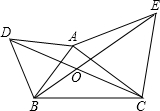 (2013•槐荫区二模)如图,△ABD与△AEC都是等边三角形,AB≠AC.下列结论中,正确的是
(2013•槐荫区二模)如图,△ABD与△AEC都是等边三角形,AB≠AC.下列结论中,正确的是查看答案和解析>>
科目:初中数学 来源:厦门市2006——2007学年(上)九年级上数学期中试题-华师大版 题型:013
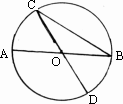
如图,AB与CD都是⊙O的直径,∠AOC=50°则∠C的度数为
A.20°
B.25°
C.30°
D.50°
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
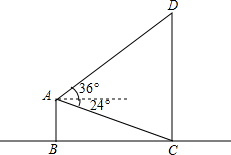 如图,AB与CD都是垂直于地面BC的建筑物.在建筑物AB的顶点A处测得建筑物CD的底端C的俯角为24°,测得顶端D的仰角为36°,若AC=200米,AD=300米,求建筑物CD的高度.(结果保留根号)
如图,AB与CD都是垂直于地面BC的建筑物.在建筑物AB的顶点A处测得建筑物CD的底端C的俯角为24°,测得顶端D的仰角为36°,若AC=200米,AD=300米,求建筑物CD的高度.(结果保留根号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com