
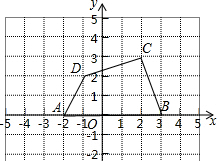
 如图,四边形ABCD的各顶点的坐标分别为A(-2,0),B(3,0),C(2,4),D(-1,2).
如图,四边形ABCD的各顶点的坐标分别为A(-2,0),B(3,0),C(2,4),D(-1,2).分析 (1)把各点横坐标加3,纵坐标不变即可得出A1、B1、C1、D1的坐标;
(2)在坐标系内描出各点,再顺次连接,根据两图形的位置即可得出结论;
(3)把各点横坐标不变,纵坐标各增加3,得到的四边形A2B2C2D2,根据两图形的位置即可得出结论.
解答 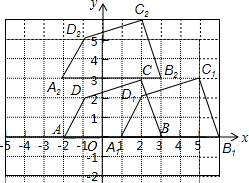 解:(1)∵A(-2,0),B(3,0),C(2,4),D(-1,2),
解:(1)∵A(-2,0),B(3,0),C(2,4),D(-1,2),
∴A1(1,0),B1(6,0),C1(5,4),D1(2,2);
(2)如图所示,由图可知四边形A1B1C1D1是原四边形ABCD向右平移3个单位而成;
(3)由图可知,四边形A2B2C2D2由四边形ABCD向上平移3个单位而成.
点评 本题考查的是作图平移变换,熟知图形平移不变性的性质是解答此题的关键.


科目:初中数学 来源: 题型:选择题
 如图,在一张地图上有A、B、C三地,A地在B地的东北方向,在C地的北偏西30°方向,则∠A等于( )
如图,在一张地图上有A、B、C三地,A地在B地的东北方向,在C地的北偏西30°方向,则∠A等于( )| A. | 60° | B. | 75° | C. | 90° | D. | 105° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图是从上面看一个由若干个相同的小正方体搭成的几何体得到的形状图,其中小正方形内的数字是该位置小正方体的个数,请你画出从正面和左面看这个几何体得到的形状图.
如图是从上面看一个由若干个相同的小正方体搭成的几何体得到的形状图,其中小正方形内的数字是该位置小正方体的个数,请你画出从正面和左面看这个几何体得到的形状图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com