
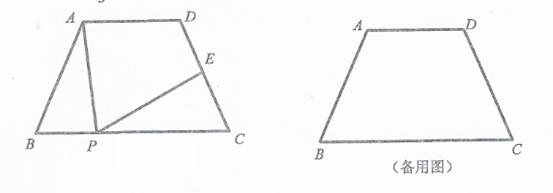
四边形 中,
中,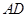 ∥
∥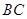 ,
,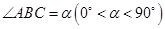 ,
,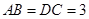 ,
,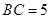 .点
.点 为射线
为射线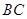 上动点(不与点
上动点(不与点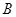 、
、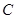 重合),点
重合),点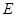 在直线
在直线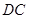 上,且
上,且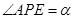 .记
.记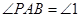 ,
,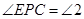 ,
,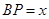 ,
,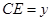 .
.
(1)当点 在线段
在线段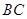 上时,写出并证明
上时,写出并证明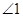 与
与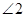 的数量关系;
的数量关系;
(2)随着点 的运动,(1)中得到的关于
的运动,(1)中得到的关于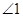 与
与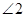 的数量关系,是否改变?若认为不改变,请证明;若认为会改变,请求出不同于(1)的数量关系,并指出相应的
的数量关系,是否改变?若认为不改变,请证明;若认为会改变,请求出不同于(1)的数量关系,并指出相应的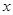 的取值范围;
的取值范围;
(3)若cos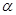 =
=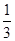 ,试用
,试用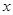 的代数式表示
的代数式表示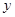 .
.
见解析
【解析】证明:(1)∠1=∠2 1分
∵∠ =∠
=∠ +∠1,又∠
+∠1,又∠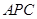 =∠
=∠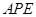 +∠2,
+∠2,
∴∠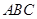 +∠1=∠
+∠1=∠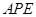 +∠2,
+∠2,
∵∠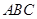 =
=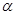 =∠
=∠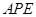 ,
,
∴∠1=∠2 2分
解:(2)会改变,当点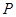 在
在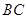 延长线上时,即
延长线上时,即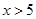 时,
1分
时,
1分
∠1与∠2的数量关系不同于(1)的数量关系。
∵∠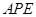 =
=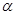 =∠
=∠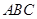 ,
,
∴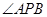 =
=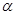 -∠2,
1分
-∠2,
1分
∵∠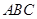 +∠
+∠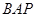 +
+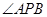 =180°,
=180°,
∴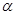 +∠1+
+∠1+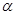 -∠2=180°,
1分
-∠2=180°,
1分
∴∠1-∠2=180°-2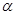 . 1分
. 1分
解:(3)情况1:当点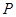 在线段
在线段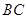 上时,
上时,
∵∠1=∠2,∠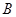 =∠
=∠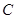 ,
,
∴△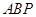 ∽△
∽△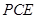 ,
1分
,
1分
∴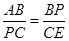 ,
1分
,
1分
即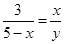 ,
,
∴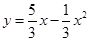 。
2分
。
2分
情况2:当点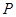 在线段
在线段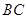 的延长线上时,
的延长线上时,
可得△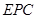 ∽△
∽△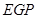 ,
,
∴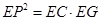 1分
1分
作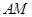 //
//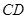 ,可得
,可得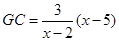
作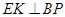 ,由
,由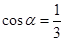 得
得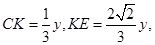
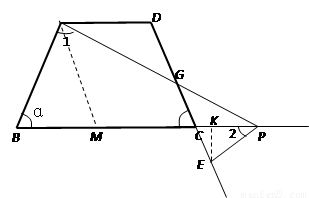

∴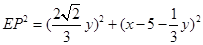 ,
,
于是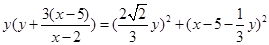
即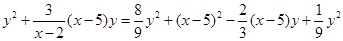
亦即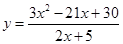 2分
2分
(1)∠APC是△ABP的外角,根据外角等于不相邻的两个内角之和易得∠1=∠2;
(2)当BP>5时,∠1与∠2的数量关系显然会改变.根据三角形内角和定理得新的关系;
(3)分两种情形分别求解.①当点P在线段BC上时,根据△ABP∽△PCE得关系求解;②当点P在线段BC的延长线上时,根据△EPC∽△EGP得关系求解.


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
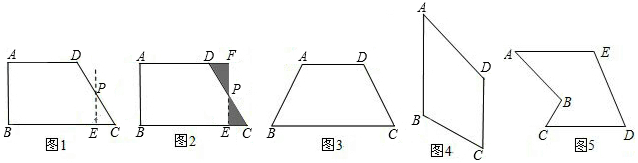
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com