
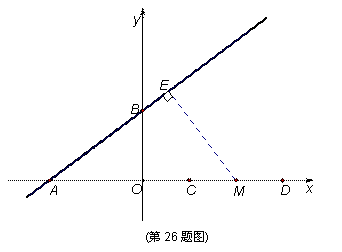
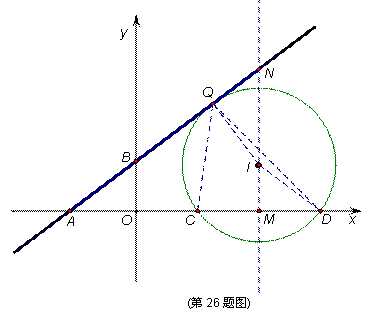
已知直线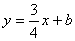 与
与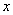 轴、
轴、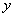 轴分别相交于
轴分别相交于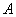 、
、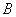 两点,点
两点,点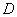 在
在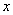 轴正半
轴正半
轴上,且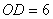 ,点
,点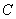 、
、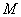 是线段
是线段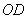 的三等分点(点
的三等分点(点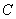 在点
在点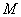 的左侧).
的左侧).
 (1)若直线
(1)若直线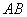 经过点
经过点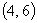 ,
,
①求直线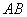 的解析式;
的解析式;
②求点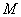 到直线
到直线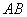 的距离;
的距离;
(2)若点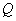 在
在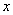 轴上方的直线
轴上方的直线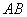 上,且
上,且
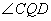 是 锐角,试探究:在直线
是 锐角,试探究:在直线
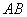 上是否存在符合条件的点
上是否存在符合条件的点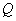 ,使
,使
得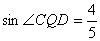 ;若存在,求出b
;若存在,求出b
的取值范围,若不存在,请说明理由.
 |
 |
解:(1) ①把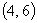 代入
代入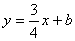 中,得:
中,得: ,解得:
,解得: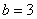 .
.
∴直线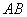 的解析式为:
的解析式为: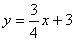 .………………………………
.……………………………… ……………………3分
……………………3分
 ②∵
②∵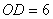 ,点
,点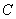 、
、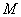 是线段
是线段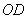 的三等分点.
的三等分点.
∴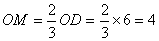 ,
,
∴点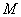 的坐标为
的坐标为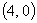 .
.
过点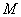 作
作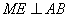 于点
于点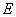 ,则
,则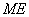 的长是点
的长是点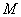 到直线
到直线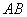 的距离.
的距离.
在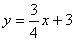 中,令
中,令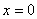 ,则
,则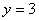 ,
,
∴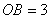 .…………………………………4分
.…………………………………4分
令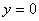 ,则
,则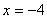 ,∴
,∴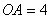 .
.
在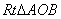 中,由勾股定理,得:
中,由勾股定理,得: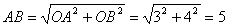 ,
,
 ,
,
在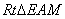 中,
中,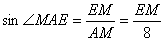 ,
, ∴
∴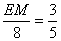 ,
,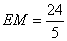 .
.
 ∴点
∴点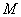 到直线
到直线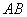 的距离为
的距离为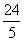 .……………………………7分
.……………………………7分
(2)在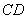 的垂直平分线上取点
的垂直平分线上取点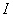 (4,1.5)
(4,1.5)
以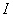 为圆心,
为圆心,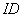 为半径作圆,则⊙
为半径作圆,则⊙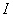 必过点
必过点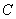 ,
,
在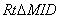 中,
中,
由勾股定理,得: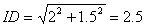 .
.
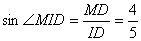 …………8分
…………8分
当直线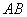 与⊙
与⊙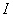 相切(切点在第一象限)时,直线
相切(切点在第一象限)时,直线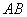
 上存在唯一一个符合条件的点
上存在唯一一个符合条件的点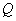 (切点),使得
(切点),使得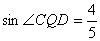 ,此时设
,此时设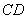 的垂直平分线交直线
的垂直平分线交直线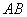 于点
于点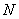 ,
,
在直线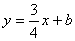 中,令
中,令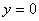 ,则
,则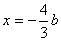 ,∴
,∴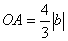 ,令
,令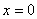 ,则
,则 ,∴
,∴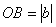 ,由勾股定理,得:
,由勾股定理,得: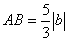 .
.
∵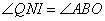 ,
,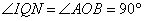 ,∴
,∴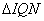 ∽
∽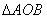 ,
,
∴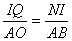 ,
,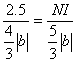 ,
,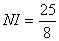 .
.
∴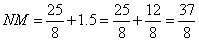 ,
,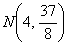 .…………………………………10分
.…………………………………10分
则把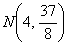 代入
代入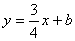 中,得:
中,得: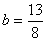 ,
,
此时直线 的解析式为:
的解析式为: .
.
若直线 过点
过点 ,则把
,则把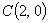 代入
代入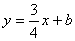 中,得:
中,得: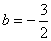 ,
,
若直线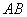 过点
过点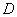 ,则把
,则把 代入
代入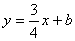 中,得:
中,得: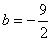 ,
,
∴当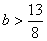 或
或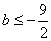 时,点
时,点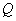 不存在;
不存在;
当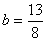 或
或 时,存在符合条件的一个点
时,存在符合条件的一个点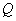 ;
;
当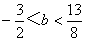 时,存在符合条件的两个点
时,存在符合条件的两个点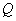 .
.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
某公司的物流业务原来由A运输队承接,已知其收费标准y(元)与运输所跑路程x(公里)之间是某种函数关系.其中部分数据如下表所示:
| x(公里) | 80 | 120 | 180 | 200 | … |
| y(元) | 200 | 300 | 450 | 500 | … |
(1)写出y(元)关于x(公里)的函数解析式 ;(不需写出定义域)
(2)由于行业竞争激烈,现B运输队表示:若公司每次支付200元的汽车租赁费,则可按每公里0.9元收费.请写出B运输队每次收费y(元)关于所跑路程x(公里)的函数解析式 ;(不需写出定义域)
(3)如果该公司有一笔路程500公里的运输业务,请通过计算说明应该选择哪家运输队?
查看答案和解析>>
科目:初中数学 来源: 题型:
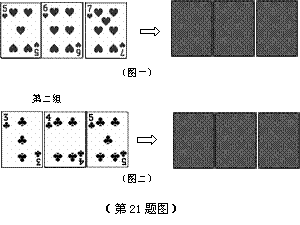
如图(一)(二),现有两组扑克牌,每组3张扑克,第一组分别是红桃5、红桃6、红桃7,第二组分别是梅花3、梅花4、梅花5.
(1)现把第一组扑克牌背面朝上并搅匀,如图(一)所示,若从第一组中随机抽取一张牌,
求“抽到红桃6”的概率;
(2)如图(一)(二),若把两组扑克牌背面朝上各自搅匀,并分别从两组中各抽取一张牌,
 试求“抽出一对牌(即数字相同)”的概率(要求用树状图或列表法求解).
试求“抽出一对牌(即数字相同)”的概率(要求用树状图或列表法求解).
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com