
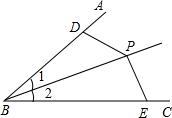
 如下图,点P为∠ABC角平分线上的一点,D点和E点分别在AB和BC上,且PD=PE,试探究∠BDP与∠BEP的数量关系,并给予证明.
如下图,点P为∠ABC角平分线上的一点,D点和E点分别在AB和BC上,且PD=PE,试探究∠BDP与∠BEP的数量关系,并给予证明. 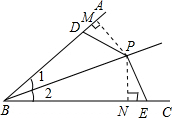 解:∠BDP+∠BEP=180°.
解:∠BDP+∠BEP=180°.
|


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:学习周报 数学 沪科九年级版 2009-2010学年 第5期 总第161期 沪科版 题型:044
如下图,点
C为线段AB的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1、S2(S1>S2),如果(1)研究小组猜想:在△ABC中,若点D为AB边上的黄金分割点(如下图),则直线CD是△ABC的黄金分割线,你认为对吗?为什么?

(2)请你说明:三角形的中线是否也是该三角形的黄金分割线?
查看答案和解析>>
科目:初中数学 来源:2007年陕西省初中毕业生学业考试数学模拟试卷(十) 题型:044
如下图,在直径为AB的半圆内,划出一块三角形区域使三角形的一边为AB,顶点C在半圆上,其他两边分别为6和8.现在建造一个内接于△ABC的矩形水池DEFN,其中DE在AB上,如图的设计方案是使AC=8,BC=6.
(1)求△ABC中AB边上的高h.
(2)设DN=x,当x为何值时,水池DEFN的面积最大?
(3)实施施工时,发现在AB上距B点1.85的M处有一棵大树,这棵大树是否位于最大矩形水池的边上?如果在,为保护大树,请设计出另外的方案,使内接于满足条件的三角形中欲建的最大矩形水池能避开这棵大树.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com