Question

如果等边三角形的边长为4，那么连接各边中点所成的三角形的周长为（ ）
A．12
B．8
C．6
D．9

Answer 1

【答案】分析：根据三角形的中位线得出DE=AC，DF=BC，EF=AB，代入△DEF的周长（DE+DF+EF）求出即可．
解答：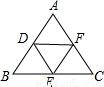
解：∵D、E、F分别是AB、BC、AC的中点，
∴DE=AC，DF=BC，EF=AB，
∴△DEF的周长是DE+DF+EF=（AC+BC+AB）=×（4+4+4）=6，
故选C．
点评：本题考查了等边三角形的性质和三角形的中位线的应用，关键是求出DE+DF+EF=（AC+BC+AB），本题比较典型，难度适中．