
分析 先计算出a1=($\frac{3}{2}$)2,a2=($\frac{7}{6}$)2,a3=($\frac{13}{12}$)2,…,an=[$\frac{n(n+1)+1}{n(n+1)}$]2,再根据二次根式的性质得到S2013=$\frac{3}{2}$+$\frac{7}{6}$+$\frac{13}{12}$+…+$\frac{2013×2014+1}{2013×2014}$,接着把分数都化成真分数,利用分式的减法运算得到S2013=2014-$\frac{1}{2014}$,然后把S2013=2014-$\frac{1}{2014}$代入$\frac{{2014×{S_{2013}}}}{2013}$中计算即可.
解答 解:∵a1=($\frac{3}{2}$)2,${a_2}=1+\frac{1}{2^2}+\frac{1}{3^2}$=($\frac{7}{6}$)2,${a_3}=1+\frac{1}{3^2}+\frac{1}{4^2}$=($\frac{13}{12}$)2,…,${a_n}=1+\frac{1}{n^2}+\frac{1}{{{{(n+1)}^2}}}$=[$\frac{n(n+1)+1}{n(n+1)}$]2,
∴S2013=$\frac{3}{2}$+$\frac{7}{6}$+$\frac{13}{12}$+…+$\frac{2013×2014+1}{2013×2014}$=2013+$\frac{1}{2}$+$\frac{1}{6}$+$\frac{1}{12}$+$\frac{1}{2013×2014}$=2013+1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2013}$-$\frac{1}{2014}$=2014-$\frac{1}{2014}$
∴$\frac{{2014×{S_{2013}}}}{2013}$=$\frac{2014×(2014-\frac{1}{2014})}{2013}$=$\frac{201{4}^{2}-1}{2013}$=$\frac{(2014+1)(2014-1)}{2013}$=2015.
故答案为2015.
点评 本题考查了二次根式的化简求值:二次根式的化简求值,一定要先化简再代入求值.二次根式运算的最后,注意结果要化到最简二次根式,二次根式的乘除运算要与加减运算区分,避免互相干扰.


科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{60y-x=2}\\{x=3-50y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{60y-x=2}\\{50y-x=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{60y=x+2}\\{50y=x-3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{60y=x-2}\\{50y=x+3}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
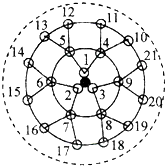 生物课题研究小组对附着在物体表面的三个微生物(课题组成员把他们分别标号为1,2,3)的生长情况进行观察记录,这三个微生物第一天各自一分为二产生新的微生物(依次标号为4,5,6,7,8,9),接下去每天都按照这样的规律变化,即每个微生物一分为二,形成新的微生物(课题组成员用如图所示的图形进行形象的记录),那么8天所出现的微生物中标号最大的数字是1533号.
生物课题研究小组对附着在物体表面的三个微生物(课题组成员把他们分别标号为1,2,3)的生长情况进行观察记录,这三个微生物第一天各自一分为二产生新的微生物(依次标号为4,5,6,7,8,9),接下去每天都按照这样的规律变化,即每个微生物一分为二,形成新的微生物(课题组成员用如图所示的图形进行形象的记录),那么8天所出现的微生物中标号最大的数字是1533号.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com