
 ��
��
 ��
��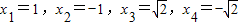 ��
�� ��Ϊԭ���̵ĸ���
��Ϊԭ���̵ĸ���


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ���ݶ���ʽ�ij˷�����ʽ�ֽ�Ĺ�ϵ���ɵ�x2-x-6=��x+2����x-3�����ұߵ�����һ������ʽ��ϵ���й�ϵ11��-32������ϡ��½���������ԭʽ��߶������ϵ�����ұ���������ԭʽ��߳����������˻�֮����ԭʽ���һ�����ϵ�������ַֽ��������ʽ�ķ����С�ʮ����˷�������ͬѧ������۲죬�����������������⣮
���ݶ���ʽ�ij˷�����ʽ�ֽ�Ĺ�ϵ���ɵ�x2-x-6=��x+2����x-3�����ұߵ�����һ������ʽ��ϵ���й�ϵ11��-32������ϡ��½���������ԭʽ��߶������ϵ�����ұ���������ԭʽ��߳����������˻�֮����ԭʽ���һ�����ϵ�������ַֽ��������ʽ�ķ����С�ʮ����˷�������ͬѧ������۲죬�����������������⣮| 2 | x2-3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015�콭��ʡ�γ������꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
����ͼ������ʾ������������ϵ��Ҳ��������������������ϵ������ͼ��������ͼ��֮��Ĺ�ϵ������˼�뷽����Ϊ���ν�ϣ����Ǹ�ѧ���ĵ�9�¡���ʽ�˷�����ʽ�ֽ⡷�ͺܺõ���������һ˼�뷽���������������ν�ϵ�˼��������������
��1����ͼ��һ���߳�Ϊ1�������Σ�����ȡ�����������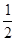 ��
�� ��
��
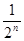 ������ͼʾ���ǿ���֪����
������ͼʾ���ǿ���֪����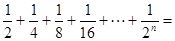 ��
��

����������ʽ���㣺 ��
��
��2�����㣺 ��
��
��3�����㣺 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ���ݶ���ʽ�ij˷�����ʽ�ֽ�Ĺ�ϵ���ɵ�x2-x-6=��x+2����x-3�����ұߵ�����һ������ʽ��ϵ���й�ϵ11��-32������ϡ��½���������ԭʽ��߶������ϵ�����ұ���������ԭʽ��߳����������˻�֮����ԭʽ���һ�����ϵ�������ַֽ��������ʽ�ķ����С�ʮ����˷�������ͬѧ������۲죬�����������������⣮
���ݶ���ʽ�ij˷�����ʽ�ֽ�Ĺ�ϵ���ɵ�x2-x-6=��x+2����x-3�����ұߵ�����һ������ʽ��ϵ���й�ϵ11��-32������ϡ��½���������ԭʽ��߶������ϵ�����ұ���������ԭʽ��߳����������˻�֮����ԭʽ���һ�����ϵ�������ַֽ��������ʽ�ķ����С�ʮ����˷�������ͬѧ������۲죬�����������������⣮ ��
���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ͬ���� ���ͣ������
| �ɶ���ʽ�ij˷�����֪������x+a����x+b��=x2+x+q����p=a+b��q=a��b��������x2+x+q=��x+a����x+b��Ҫ������ʽx2+x+q���зֽ⣬�ؼ����ҵ�������a��b��ʹa+b=p��a��b=q����Զ���ʽx2-3x+2����p=-3��q=2��a=-1��b=-2����ʱ��-1��+��-2��=-3����-1����-2��=2������x2-3x+2�ɷֽ�Ϊ��x-1����x-2����x2-3x-2=��x-1����x-2���� ��1������������д�±��� | ||||||||||||||||||||||||||||||
��q������ʱ��Ӧ�ֽ����������a��b_______________�ţ�a��b�ķ�����__________��ͬ�� ��q�Ǹ���ʱ��Ӧ�ֽ�ɵ���������a��b______________�ţ�a��b�о���ֵ�ϴ�������ķ�����_______��ͬ�� ��3���ֽ���ʽ�� x2-x-12=_____________��x2-7x+6=________________�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com