练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下列计算正确的是（ ）
    A.5a+2a=7a2
    B.5a﹣2a=3
    C.5a﹣2a=3a
    D.﹣ab+2ab2=ab2

    【答案】C
    【解析】解：A、5a+2a=7a，故此选项错误；

    B、5a﹣2a=3a，故此选项错误；

    C、5a﹣2a=3a，正确；

    D、﹣ab+2ab2，无法计算，故此选项错误．

    故选：C．

    【考点精析】根据题目的已知条件，利用合并同类项的相关知识可以得到问题的答案，需要掌握在合并同类项时，我们把同类项的系数相加，字母和字母的指数不变．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如果x﹣y=5且y﹣z=5，那么x﹣z的值是（ ）
    A.5
    B.10
    C.﹣5
    D.﹣10

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在社会实践活动中，某中学对甲、乙，丙、丁四个超市三月份的苹果价格进行调查．它们的价格的平均值均为3.50元，方差分别为S甲2=0.3，S乙2=0.4，S丙2=0.1，S丁2=0.25．三月份苹果价格最稳定的超市是（ ）
    A.甲
    B.乙
    C.丙
    D.丁

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动：将△MNK的直角顶点M放在△ABC的斜边AB的中点处，设AC=BC=a．

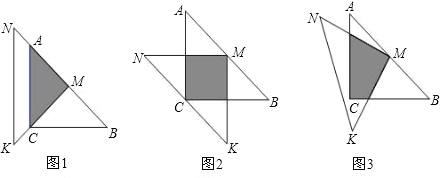
    （1）如图1，两个三角尺的重叠部分为△ACM，则重叠部分的面积为 ,周长为 .

    （2）将图1中的△MNK绕顶点M逆时针旋转45°，得到图2，此时重叠部分的面积为 ,周长为 .

    2（3）如果将△MNK绕M旋转到不同于图1，图2的位置，如图3所示，猜想此时重叠部分的面积为多少？并试着加以验证．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知AC⊥BC，BD⊥AD，AC 与BD 交于O，AC=BD．

    求证：（1）BC=AD；

    （2）△OAB是等腰三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列正确说法的个数是（ ）

    ①同位角相等；②等角的补角相等；③两直线平行，同旁内角相等；④在同一平面内，过一点有且只有一条直线与已知直线垂直．

    A.1B.2C.3D.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】探究;

    （）如图， 、为的边、上的两定点，在上求作一点，使的周长最短．（不写作法）

    （）如图，矩形中， ， ， 、分别为边、的中点，点、分别为、上的动点，求四边形周长的最小值．

    （）如图，正方形的边长为，点为边中点，在边、、上分别确定点、、．使得四边形周长最小，并求出最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】矩形纸片ABCD中，已知AD=8，AB=6，E是边BC上的点，以AE为折痕折叠纸片，使点B落在点F处，连接FC，当△EFC为直角三角形时，BE的长为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（本小题满分10分）

    观察思考

    某种在同一平面进行传动的机械装置如图14-1，图14-2是它的示意图．其工作原理是：滑块Q在平直滑道l上可以左右滑动，在Q滑动的过程中，连杆PQ也随之运动，并且PQ带动连杆OP绕固定点O摆动．在摆动过程中，两连杆的接点P在以OP为半径的⊙O上运动．数学兴趣小组为进一步研究其中所蕴含的数学知识，过点O作OH ⊥l于点H，并测得OH = 4分米，PQ = 3分米，OP = 2分米．

    解决问题

    （1）点Q与点O间的最小距离是 分米；点Q与点O间的最大距离是 分米；点Q在l上滑到最左端的位置与滑到最右端位置间的距离是 分米．

    （2）

    如图14-3，小明同学说：“当点Q滑动到点H的位置时，PQ与⊙O是相切的．”你认为他的判断对吗？为什么？

    （3）①小丽同学发现：“当点P运动到OH上时，点P到l的距离最小．”事实上，还存在着点P到l距离最大的位置，此时，点P到l的距离是 分米；

    ②当OP绕点O左右摆动时，所扫过的区域为扇形，求这个扇形面积最大时圆心角的度数．

    查看答案和解析>>

    同步练习册答案