
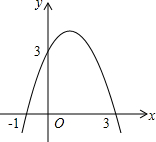
 二次函数y=-x2+2x+3的图象如图所示,在x轴上方,且平行于x轴的直线与该二次函数的图象交于M,N两点,在x轴上取点Q,使△MNQ为等腰直角三角形,请你写出所有符合的点Q的坐标(1,0)或(2-$\sqrt{5}$,0)或($\sqrt{5}$,0).
二次函数y=-x2+2x+3的图象如图所示,在x轴上方,且平行于x轴的直线与该二次函数的图象交于M,N两点,在x轴上取点Q,使△MNQ为等腰直角三角形,请你写出所有符合的点Q的坐标(1,0)或(2-$\sqrt{5}$,0)或($\sqrt{5}$,0). 分析 此题要分三种情况讨论:
①点Q是直角顶点,那么点Q必为抛物线对称轴与x轴的交点,由此求得点Q的坐标;
②以M为直角顶点时,可Q2(x,0)(x<1),根据抛物线的对称性可知MN正好等于抛物线对称轴到M点距离的2倍,而△MNQ是等腰直角三角形,则QM=MN,由此可表示出点M的纵坐标,联立抛物线的解析式,即可得到关于M点横坐标的方程,从而求得点Q的坐标;\
③以N为直角顶点时,根据抛物线的对称性知:Q关于抛物线的对称点也符合题意;
解答 解:存在,且Q的坐标为(1,0)或(2-$\sqrt{5}$,0)或($\sqrt{5}$,0);
由二次函数y=-x2+2x+3可知抛物线与x轴的交点为(-1,0),(3,0),
∴对称轴为x=$\frac{-1+3}{2}$=1,
①若Q是直角顶点,由M、N对称性可直接得Q1(1,0);
②若M是直角顶点;
设Q2(x,0)(x<1),
∴MN=2Q1Q2=2(1-x),
∵△Q2MN为等腰直角三角形;
∴y=2(1-x)即-x2+2x+3=2(1-x);
∵x<1,
∴Q2(2-$\sqrt{5}$,0);
③若N是直角顶点;
由对称性可得Q3($\sqrt{5}$,0);
故Q点的坐标为(1,0)或(2-$\sqrt{5}$,0)或($\sqrt{5}$,0).
点评 此题主要考查了二次函数的性质、等腰三角形及等腰直角三角形的判定和性质,分类讨论的数学思想是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 209×108元 | B. | 209×109元 | C. | 2.09×1010元 | D. | 2.09×1011元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
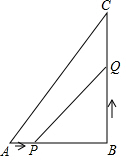 如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点 A 开始沿边AB向B 以lcm/s的速度移动,点Q从点B开始沿边BC向点C以2cm/s的速度移动,如果点P、Q分别同时从A、B出发.
如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点 A 开始沿边AB向B 以lcm/s的速度移动,点Q从点B开始沿边BC向点C以2cm/s的速度移动,如果点P、Q分别同时从A、B出发.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x(℃) | … | -10 | 0 | 10 | 20 | 30 | … |
| y(℉) | … | 14 | 32 | 50 | 68 | 86 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com