
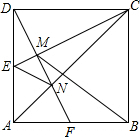
 如图,在正方形ABCD中,E为AD的中点,DF⊥CE于M,交AC于点N,交AB于点F,连接EN、BM.有如下结论:①△ADF≌△DCE;②MN=FN;③△DMC∽△EMN;④BM=AB;其中正确结论的个数为( )
如图,在正方形ABCD中,E为AD的中点,DF⊥CE于M,交AC于点N,交AB于点F,连接EN、BM.有如下结论:①△ADF≌△DCE;②MN=FN;③△DMC∽△EMN;④BM=AB;其中正确结论的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①本题需先根据已知条件,得出∠ADF=∠DCE,即可判定△ADF与△DCE全等.
②本题需先根据AE=AF,∠NAF=∠NAE,AN=AN这三个条件,得出△ANF≌△ANE,即可得出NF>MN.
③根据$\frac{DM}{CM}≠\frac{EM}{NM}$,而∠CMD=∠NME,即可得出△DMC∽△EMN不成立.
④延长DF与CB交于G,则∠ADF=∠G,根据直角三角形斜边上中线的性质,即可得到BM=$\frac{1}{2}$CG=BC,进而得出BM=AB.
解答 解:①∵DF⊥CE,∠CDE=90°,
∴∠ADF+∠CDF=∠DCE+∠CDF,
∴∠ADF=∠DCE,
在△ADF和△DCE中,
$\left\{\begin{array}{l}{∠DAF=∠EDC}\\{AD=DC}\\{∠ADF=∠DCE}\end{array}\right.$,
∴△ADF≌△DCE(ASA),
故①正确;
②∵△ADF≌△DCE,
∴DE=AF,
∵AE=DE,
∴AE=AF,
在△ANF和△ANE中
$\left\{\begin{array}{l}{AE=AF}\\{∠NAF=∠NAE}\\{AN=AN}\end{array}\right.$,
∴△ANF≌△ANE(SAS),
∴NF=NE,
∵NM⊥CE,
∴Rt△MEN中,NE>MN,
∴NF>MN,
∴MN=FN不成立,
故②错误;
③设DE=AF=1,则CD=2,
∴CE=DF=$\sqrt{5}$,
∵DM⊥CE,
∴$\frac{1}{2}$DE×CD=$\frac{1}{2}$CE×DM,
∴DM=$\frac{DE×CD}{CE}$=$\frac{2}{5}\sqrt{5}$,EM=$\sqrt{D{E}^{2}-D{M}^{2}}$=$\frac{1}{5}\sqrt{5}$,
∴CM=$\sqrt{5}$-$\frac{1}{5}\sqrt{5}$=$\frac{4}{5}\sqrt{5}$,
∴DM:CM=1:2,
∵AF∥CD,
∴$\frac{AF}{CD}=\frac{FN}{DN}=\frac{1}{2}$,
∴DN=$\frac{2}{3}$DF=$\frac{2}{3}\sqrt{5}$,
∴MN=DN-DM=$\frac{4}{15}\sqrt{5}$,
∴EM:MN=3:4,
∴$\frac{DM}{CM}≠\frac{EM}{NM}$,而∠CMD=∠NME,
∴△DMC∽△EMN不成立,
故③错误;
④如图,延长DF与CB交于G,则∠ADF=∠G,
根据F为AB中点,可得AF=BF,
在△DAF与△GBF中,
$\left\{\begin{array}{l}{∠ADF=∠G}\\{∠DAB=∠GBF=90°}\\{AF=BF}\end{array}\right.$,
∴△DAF≌△GBF(AAS),
∴BG=AD,
又∵AD=BC,
∴BC=BG,
∴Rt△CMG中,BM=$\frac{1}{2}$CG=BC,
又∵BC=AB,
∴MB=AB,
故④正确;
故选:B.
点评 本题主要考查了正方形的性质,全等三角形的判定与性质,相似三角形的判定与性质以及勾股定理的运用,在解题时要注意全等三角形的对应边相等、相似三角形的对应边成比例.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2017届山东省济南市天桥区九年级学业水平考试第一次模拟数学试卷(解析版) 题型:填空题
如图,点A为函数y= (x>0)图象上一点,连接OA,交函数y=
(x>0)图象上一点,连接OA,交函数y= (x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为________________.
(x>0)的图象于点B,点C是x轴上一点,且AO=AC,则△ABC的面积为________________.
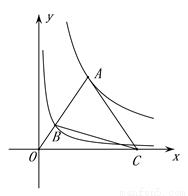
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
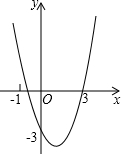 如图,抛物线过(-1,0),(3,0),(0,-3)三点,沿x轴方向平移抛物线,使得以平移后的抛物线与x轴、y轴的三个交点为顶点的三角形面积为4,则符合条件的平移方式有( )
如图,抛物线过(-1,0),(3,0),(0,-3)三点,沿x轴方向平移抛物线,使得以平移后的抛物线与x轴、y轴的三个交点为顶点的三角形面积为4,则符合条件的平移方式有( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
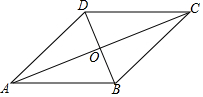 如图,在菱形ABCD中,对角线AC与BD相交于点O,若∠ADC=130°,则∠DAC的大小为( )
如图,在菱形ABCD中,对角线AC与BD相交于点O,若∠ADC=130°,则∠DAC的大小为( )| A. | 75° | B. | 65° | C. | 25° | D. | 50° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
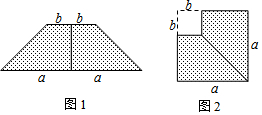
| A. | (a+b)(a-b)=a2-b2 | B. | (a-b)2=a2-2ab+b2 | ||
| C. | (a+b)2=a2+2ab+b2 | D. | (a+2b)(a-b)=a2+ab-2b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
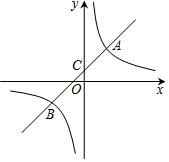 如图,一次函数y=x+b的图象与反比例函数y=$\frac{k}{x}$的图象交于点A(3,6)与点B,且与y轴交于点C,若点P是反比例函数y=$\frac{k}{x}$图象上的一个动点,作直线AP与x轴、y轴分别交于点M、N,连结BN、CM.若S△ACM=S△ABN,则$\frac{AP}{AN}$的值为2或4.
如图,一次函数y=x+b的图象与反比例函数y=$\frac{k}{x}$的图象交于点A(3,6)与点B,且与y轴交于点C,若点P是反比例函数y=$\frac{k}{x}$图象上的一个动点,作直线AP与x轴、y轴分别交于点M、N,连结BN、CM.若S△ACM=S△ABN,则$\frac{AP}{AN}$的值为2或4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
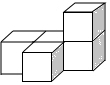 如图是由五个完全相同的小正方体组成的几何体,若将最左边的小正方体拿掉,则下列结论正确的是( )
如图是由五个完全相同的小正方体组成的几何体,若将最左边的小正方体拿掉,则下列结论正确的是( )| A. | 主视图不变 | B. | 左视图不变 | C. | 俯视图不变 | D. | 三视图不变 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2•x3=x6 | B. | $\sqrt{{x}^{2}}$=x | C. | $\frac{{x}^{2}-x}{x}$=x-1 | D. | x2-x+1=(x-$\frac{1}{2}$)2+$\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com