
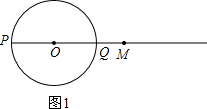
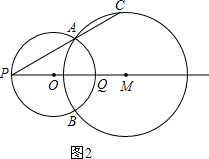
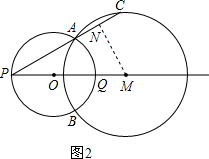
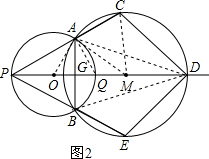
 解:(1)过点M作MN⊥AC,垂足为N,
解:(1)过点M作MN⊥AC,垂足为N,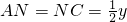 ,
,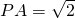 ,
, ,
,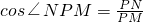 ,
,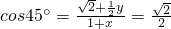 ,
,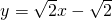 (x>1),
(x>1),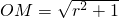
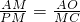 ,即
,即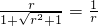 ,解得
,解得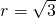 ,
, .
.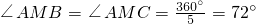 ,∠BAC=108°,
,∠BAC=108°,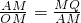
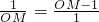 ,解得:
,解得: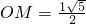 (负值舍去)
(负值舍去)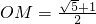 ,
,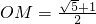 ,圆M的半径是1.
,圆M的半径是1.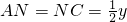 ,再根据PM⊥AB,又AB是圆O的直径,可得
,再根据PM⊥AB,又AB是圆O的直径,可得 ,在Rt△PNM中,再利用
,在Rt△PNM中,再利用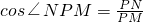 即可求得y关于x的函数解析式;
即可求得y关于x的函数解析式;

 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:
 3、司机在驾驶汽车时,发现紧急情况到踩下刹车需要一段时间,这段时间叫反应时间.之后还会继续行驶一段距离.我们把司机从发现紧急情况到汽车停止所行驶的这段距离叫“刹车距离”(如图).
3、司机在驾驶汽车时,发现紧急情况到踩下刹车需要一段时间,这段时间叫反应时间.之后还会继续行驶一段距离.我们把司机从发现紧急情况到汽车停止所行驶的这段距离叫“刹车距离”(如图).查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 司机在驾驶汽车时,发现紧急情况到踩下刹车需要一段时间,这段时间叫反应时间.之后还会继续行驶一段距离.我们把司机从发现紧急情况到汽车停止所行驶的这段距离叫“刹车距离”(如图).
司机在驾驶汽车时,发现紧急情况到踩下刹车需要一段时间,这段时间叫反应时间.之后还会继续行驶一段距离.我们把司机从发现紧急情况到汽车停止所行驶的这段距离叫“刹车距离”(如图).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
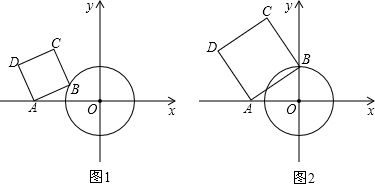
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com